Warburg coefficient

The Warburg coefficient (or Warburg constant), 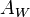$A_W$ , is the diffusion coefficient of ions in solution, associated to the Warburg element, 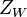$Z_W$ . The Warburg coefficient, 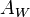$A_W$ , also written as, 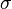${\sigma}$ , has the units of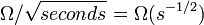 ${\Omega}/\sqrt{seconds}={\Omega}(s^{-1/2})$

The value of 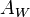$A_W$ can be obtained by the gradient of the Warburg plot, a linear plot of the real impedance ( 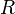$R$ ) against the reciprocal of the square root of the frequency ( 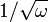${1}/\sqrt{\omega}$ ). This relation should always yield a straight line, as it is unique for a Warburg.

Alternatively, the value of 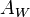$A_W$ can be found by:

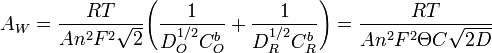
$A_W={\frac{R T}{An^2F^2\sqrt2}}{\left(\frac{1}{D_O^{1/2}C_O^b}+{\frac{1}{D_R^{1/2}C_R^b}}\right)}=\frac{R T}{An^2F^2\Theta C\sqrt{2D}}$

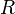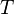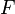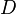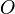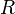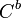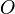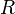where $R$ is the ideal gas constant, $T$ is the thermodynamic temperature, $F$ is the Faraday constant, $n$ is the valency, $D$ is the diffusion coefficient of the species where subscripts $O$ and $R$ stand for the oxidized and reduced species respectively, $C^b$ is the concentration of the $O$ and $R$ species in the bulk, C is the concentration of the electrolyte, 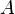$A$ denotes the surface area and 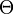$\Theta$ denotes the fraction of the 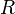$R$ and $O$ 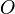species present.

The equation for 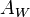$A_W$ applies to both reversible and quasi-reversible reactions for which both halves of the couple are soluble.

References

A. Ottova-Leitmannova, Advances in Planar Lipid Bilayers and Liposomes, Academic Press (2006)

This article is issued from Wikipedia - version of the 10/13/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.