Walsh matrix

Walsh matrix of order 16 multiplied with a vector

Natural ordered Hadamard matrix permuted into sequency ordered Hadamard matrix The number of sign changes per row in the natural ordered matrix is
(0,15, 7,8, 3,12, 4,11, 1,14, 6,9, 2,13, 5,10),
in the sequency ordered matrix the number of sign changes is consecutive.

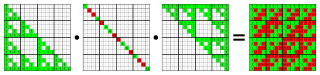
LDU decomposition of a Walsh matrix
The ones in the triangular matrices form Sierpinski triangles. The entries of the diagonal matrix are values from Gould's sequence, with the minus signs distributed like the ones in Thue–Morse sequence.

Binary Walsh matrix as a matrix product
The binary matrix (white 0, red 1) is the result with operations in F₂. The gray numbers show the result with operations in R.

In mathematics, a Walsh matrix is a specific square matrix with dimensions of some power of 2, entries of ±1, and the property that the dot product of any two distinct rows (or columns) is zero. The Walsh matrix was proposed by Joseph L. Walsh in 1923.^[1] Each row of a Walsh matrix corresponds to a Walsh function.

The natural ordered Hadamard matrix is defined by the recursive formula below, and the sequency ordered Hadamard matrix is formed by rearranging the rows so that the number of sign-changes in a row is in increasing order.^[1] Confusingly, different sources refer to either matrix as the Walsh matrix.

The Walsh matrix (and Walsh functions) are used in computing the Walsh transform and have applications in the efficient implementation of certain signal processing operations.

Formula

The Hadamard matrices of dimension 2^k for k ∈ N are given by the recursive formula

The lowest order of Hadamard matrix is 2

H(2^{1})={\begin{bmatrix}1&1\\1&-1\end{bmatrix}},

H(2^{2})={\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\\\end{bmatrix}},

and in general

H(2^{k})={\begin{bmatrix}H(2^{{k-1}})&H(2^{{k-1}})\\H(2^{{k-1}})&-H(2^{{k-1}})\end{bmatrix}}=H(2)\otimes H(2^{{k-1}}),

for 2 ≤ k ∈ N, where $\otimes$ denotes the Kronecker product.

Permutation

rearrange the rows of Matrix according the number of sign change of each row. for example:

W(4)={\begin{bmatrix}1&1&1&1\\1&-1&1&-1\\1&1&-1&-1\\1&-1&-1&1\\\end{bmatrix}}

the successive rows have 0, 3, 1, and 2 sign changes, then we rearrange the rows in sequency ordering.

e.g.

H(4)={\begin{bmatrix}1&1&1&1\\1&1&-1&-1\\1&-1&-1&1\\1&-1&1&-1\\\end{bmatrix}}

where the successive rows have 0, 1, 2, and 3 sign changes.

Alternative Forms of the Walsh Matrix

Sequency ordering

The sequency ordering of the rows of the Walsh matrix can be derived from the ordering of the Hadamard matrix by first applying the bit-reversal permutation and then the Gray code permutation.^[2]

e.g.

W(8)={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&1&1&1&-1&-1&-1&-1\\1&1&-1&-1&-1&-1&1&1\\1&1&-1&-1&1&1&-1&-1\\1&-1&-1&1&1&-1&-1&1\\1&-1&-1&1&-1&1&1&-1\\1&-1&1&-1&-1&1&-1&1\\1&-1&1&-1&1&-1&1&-1\\\end{bmatrix}}

where the successive rows have 0, 1, 2, 3, 4, 5, 6, and 7 sign changes.

Dyadic ordering

W(8)={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&1&1&1&-1&-1&-1&-1\\1&1&-1&-1&1&1&-1&-1\\1&1&-1&-1&-1&-1&1&1\\1&-1&1&-1&1&-1&1&-1\\1&-1&1&-1&-1&1&-1&1\\1&-1&-1&1&1&-1&-1&1\\1&-1&-1&1&-1&1&1&-1\\\end{bmatrix}}

where the successive rows have 0, 1, 3, 2, 7, 6, 4, and 5 sign changes.

Natural ordering

W(8)={\begin{bmatrix}1&1&1&1&1&1&1&1\\1&-1&1&-1&1&-1&1&-1\\1&1&-1&-1&1&1&-1&-1\\1&-1&-1&1&1&-1&-1&1\\1&1&1&1&-1&-1&-1&-1\\1&-1&1&-1&-1&1&-1&1\\1&1&-1&-1&-1&-1&1&1\\1&-1&-1&1&-1&1&1&-1\\\end{bmatrix}}

where the successive rows have 0, 7, 3, 4, 1, 6, 2, and 5 sign changes.

Notes

1 2 Kanjilal, P.P. (1995). Adaptive Prediction and Predictive Control. Stevenage: IET. p. 210. ISBN 0-86341-193-2.
↑ Yuen, C.-K. (1972). "Remarks on the Ordering of Walsh Functions". IEEE Transactions on Computers. 21 (12): 1452. doi:10.1109/T-C.1972.223524.

This article is issued from Wikipedia - version of the 11/1/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.