Top quark

Top quark

A collision event involving top quarks
Composition Elementary particle
Statistics Fermionic
Generation Third
Interactions Strong, Weak, Electromagnetic force, Gravity
Symbol
t
Antiparticle Top antiquark (
t
)
Theorized Makoto Kobayashi and Toshihide Maskawa (1973)
Discovered CDF and DØ collaborations (1995)
Mass 172.44 ± 0.13 (stat) ± 0.47 (syst)GeV/c2[1]
Decays into bottom quark (99.8%)
strange quark (0.17%)
down quark (0.007%)
Electric charge +2/3 e
Color charge Yes
Spin 1/2
Topness 1
Weak isospin LH: +1/2, RH: 0
Weak hypercharge LH: +1/3, RH: +4/3

The top quark, also known as the t quark (symbol: t) or truth quark, is the most massive of all observed elementary particles. Like all quarks, the top quark is an elementary fermion with spin 1/2, and experiences all four fundamental interactions: gravitation, electromagnetism, weak interactions, and strong interactions. It has an electric charge of +2/3 e,[2] It has a large mass of 172.44 ± 0.13 (stat) ± 0.47 (syst)GeV/c2,[1] which is about the same mass as an atom of tungsten. The antiparticle of the top quark is the top antiquark (symbol: t, sometimes called antitop quark or simply antitop), which differs from it only in that some of its properties have equal magnitude but opposite sign.

The top quark interacts primarily by the strong interaction, but can only decay through the weak force. It decays to a W boson and either a bottom quark (most frequently), a strange quark, or, on the rarest of occasions, a down quark. The Standard Model predicts its mean lifetime to be roughly 5×10−25 s.[3] This is about a twentieth of the timescale for strong interactions, and therefore it does not form hadrons, giving physicists a unique opportunity to study a "bare" quark (all other quarks hadronize, meaning that they combine with other quarks to form hadrons, and can only be observed as such). Because it is so massive, the properties of the top quark allow predictions to be made of the mass of the Higgs boson under certain extensions of the Standard Model (see Mass and coupling to the Higgs boson below). As such, it is extensively studied as a means to discriminate between competing theories.

Its existence (and that of the bottom quark) was postulated in 1973 by Makoto Kobayashi and Toshihide Maskawa to explain the observed CP violations in kaon decay,[4] and was discovered in 1995 by the CDF[5] and DØ[6] experiments at Fermilab. Kobayashi and Maskawa won the 2008 Nobel Prize in Physics for the prediction of the top and bottom quark, which together form the third generation of quarks.[7]

History

In 1973, Makoto Kobayashi and Toshihide Maskawa predicted the existence of a third generation of quarks to explain observed CP violations in kaon decay.[4] The names top and bottom were introduced by Haim Harari in 1975,[8][9] to match the names of the first generation of quarks (up and down) reflecting the fact that the two were the 'up' and 'down' component of a weak isospin doublet.[10] The top quark was sometimes called truth quark in the past, but over time top quark became the predominant use.[11]

The proposal of Kobayashi and Maskawa heavily relied on the GIM mechanism put forward by Sheldon Lee Glashow, John Iliopoulos and Luciano Maiani,[12] which predicted the existence of the then still unobserved charm quark. When in November 1974 teams at Brookhaven National Laboratory (BNL) and the Stanford Linear Accelerator Center (SLAC) simultaneously announced the discovery of the J/ψ meson, it was soon after identified as a bound state of the missing charm quark with its antiquark. This discovery allowed the GIM mechanism to become part of the Standard Model.[13] With the acceptance of the GIM mechanism, Kobayashi and Maskawa's prediction also gained in credibility. Their case was further strengthened by the discovery of the tau by Martin Lewis Perl's team at SLAC between 1974 and 1978.[14] This announced a third generation of leptons, breaking the new symmetry between leptons and quarks introduced by the GIM mechanism. Restoration of the symmetry implied the existence of a fifth and sixth quark.

It was in fact not long until a fifth quark, the bottom, was discovered by the E288 experiment team, led by Leon Lederman at Fermilab in 1977.[15][16][17] This strongly suggested that there must also be a sixth quark, the top, to complete the pair. It was known that this quark would be heavier than the bottom, requiring more energy to create in particle collisions, but the general expectation was that the sixth quark would soon be found. However, it took another 18 years before the existence of the top was confirmed.[18]

Early searches for the top quark at SLAC and DESY (in Hamburg) came up empty-handed. When, in the early eighties, the Super Proton Synchrotron (SPS) at CERN discovered the W boson and the Z boson, it was again felt that the discovery of the top was imminent. As the SPS gained competition from the Tevatron at Fermilab there was still no sign of the missing particle, and it was announced by the group at CERN that the top mass must be at least 41 GeV/c2. After a race between CERN and Fermilab to discover the top, the accelerator at CERN reached its limits without creating a single top, pushing the lower bound on its mass up to 77 GeV/c2.[18]

The Tevatron was (until the start of LHC operation at CERN in 2009) the only hadron collider powerful enough to produce top quarks. In order to be able to confirm a future discovery, a second detector, the DØ detector, was added to the complex (in addition to the Collider Detector at Fermilab (CDF) already present). In October 1992, the two groups found their first hint of the top, with a single creation event that appeared to contain the top. In the following years, more evidence was collected and on April 22, 1994, the CDF group submitted their paper presenting tentative evidence for the existence of a top quark with a mass of about 175 GeV/c2. In the meantime, DØ had found no more evidence than the suggestive event in 1992. A year later, on March 2, 1995, after having gathered more evidence and a reanalysis of the DØ data (who had been searching for a much lighter top), the two groups jointly reported the discovery of the top with a certainty of 99.9998% at a mass of 176±18 GeV/c2.[5][6][18]

In the years leading up to the top quark discovery, it was realized that certain precision measurements of the electroweak vector boson masses and couplings are very sensitive to the value of the top quark mass. These effects become much larger for higher values of the top mass and therefore could indirectly see the top quark even if it could not be directly detected in any experiment at the time. The largest effect from the top quark mass was on the T parameter and by 1994 the precision of these indirect measurements had led to a prediction of the top quark mass to be between 145 GeV/c2 and 185 GeV/c2.[19] It is the development of techniques that ultimately allowed such precision calculations that led to Gerardus 't Hooft and Martinus Veltman winning the Nobel Prize in physics in 1999.[20][21]

Properties

Production

Because top quarks are very massive, large amounts of energy are needed to create one. The only way to achieve such high energies is through high energy collisions. These occur naturally in the Earth's upper atmosphere as cosmic rays collide with particles in the air, or can be created in a particle accelerator. In 2011, after the Tevatron ceased operations, the Large Hadron Collider at CERN became the only accelerator that generates a beam of sufficient energy to produce top quarks, with a center-of-mass energy of 7 TeV. There are multiple processes that can lead to the production of top quarks, but they can be conceptually divided in two categories.

Top-quark pairs

gluon-gluon fusion
t-channel
quark-antiquark annihilation

The most common is production of a top–antitop pair via strong interactions. In a collision, a highly energetic gluon is created, which subsequently decays into a top and antitop. This process was responsible for the majority of the top events at Tevatron and was the process observed when the top was first discovered in 1995.[24] It is also possible to produce pairs of top–antitop through the decay of an intermediate photon or Z-boson. However, these processes are predicted to be much rarer and have a virtually identical experimental signature in a hadron collider like Tevatron.

Single top quarks

s-channel
t-channel
tW channel

A distinctly different process is the production of single top quarks via weak interaction. This can happen in several ways (called channels): either an intermediate W-boson decays into a top and antibottom quark ("s-channel") or a bottom quark (probably created in a pair through the decay of a gluon) transforms to a top quark by exchanging a W-boson with an up or down quark ("t-channel"). A single top quark can also be produced in association with a W boson, requiring an initial state bottom quark ("tW-channel"). The first evidence for these processes was published by the DØ collaboration in December 2006,[25] and in March 2009 the CDF[26] and DØ[24] collaborations released twin papers with the definitive observation of these processes. The main significance of measuring these production processes is that their frequency is directly proportional to the | Vtb |2 component of the CKM matrix.

Decay

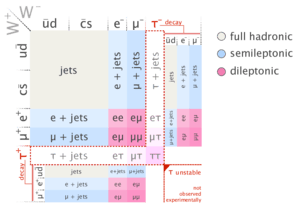
ttbar-decay final states
All possible final states of the decay of a top-quark pair

Because of its enormous mass, the top quark is extremely short-lived with a predicted lifetime of only 5×10−25 s.[3] As a result, top quarks do not have time to form hadrons before they decay, as other quarks do which provides physicists with the unique opportunity to study the behavior of a "bare" quark. The only known way the top quark can decay is through the weak interaction producing a W-boson and a down-type quark (down, strange, or bottom).

In particular, it is possible to directly determine the branching ratio Γ(W+b) / Γ(W+q (q = b,s,d)). The best current determination of this ratio is 0.91±0.04.[27] Since this ratio is equal to | Vtb |2 according to the Standard Model, this gives another way of determining the CKM element | Vtb |, or in combination with the determination of | Vtb | from single top production provides tests for the assumption that the CKM matrix is unitary.[28]

The Standard Model also allows more exotic decays, but only at one loop level, meaning that they are extremely suppressed. In particular, it is possible for a top quark to decay into another up-type quark (an up or a charm) by emitting a photon or a Z-boson.[29] Searches for these exotic decay modes have provided no evidence for their existence in accordance with expectations from the Standard Model. The branching ratios for these decays have been determined to be less than 5.9 in 1,000 for photonic decay and less than 2.1 in 1,000 for Z-boson decay at 95% confidence.[27]

Mass and coupling to the Higgs boson

The Standard Model describes fermion masses through the Higgs mechanism. The Higgs boson has a Yukawa coupling to the left- and right-handed top quarks. After electroweak symmetry breaking (when the Higgs acquires a vacuum expectation value), the left- and right-handed components mix, becoming a mass term.

The top quark Yukawa coupling has a value of

where v = 246 GeV is the value of the Higgs vacuum expectation value.

Yukawa couplings

In the Standard Model, all of the quark and lepton Yukawa couplings are small compared to the top quark Yukawa coupling. Understanding this hierarchy in the fermion masses is an open problem in theoretical physics. Yukawa couplings are not constants and their values change depending on the energy scale (distance scale) at which they are measured. The dynamics of Yukawa couplings are determined by the renormalization group equation.

One of the prevailing views in particle physics is that the size of the top quark Yukawa coupling is determined by the renormalization group, leading to the "quasi-infrared fixed point."

The Yukawa couplings of the up, down, charm, strange and bottom quarks, are hypothesized to have small values at the extremely high energy scale of grand unification, 1015 GeV. They increase in value at lower energy scales, at which the quark masses are generated by the Higgs. The slight growth is due to corrections from the QCD coupling. The corrections from the Yukawa couplings are negligible for the lower mass quarks.

If, however, a quark Yukawa coupling has a large value at very high energies, its Yukawa corrections will evolve and cancel against the QCD corrections. This is known as a (quasi-) infrared fixed point. No matter what the initial starting value of the coupling is, if it is sufficiently large it will reach this fixed point value. The corresponding quark mass is then predicted.

The top quark Yukawa coupling lies very near the infrared fixed point of the Standard Model. The renormalization group equation is:

where g3 is the color gauge coupling, g2 is the weak isospin gauge coupling, and g1 is the weak hypercharge gauge coupling. This equation describes how the Yukawa coupling changes with energy scale μ. Solutions to this equation for large initial values yt cause the right-hand side of the equation to quickly approach zero, locking yt to the QCD coupling g3. The value of the fixed point is fairly precisely determined in the Standard Model, leading to a top quark mass of 230 GeV. However, if there is more than one Higgs doublet, the mass value will be reduced by Higgs mixing angle effects in an unpredicted way.

In the minimal supersymmetric extension of the Standard Model (MSSM), there are two Higgs doublets and the renormalization group equation for the top quark Yukawa coupling is slightly modified:

where yb is the bottom quark Yukawa coupling. This leads to a fixed point where the top mass is smaller, 170–200 GeV. The uncertainty in this prediction arises because the bottom quark Yukawa coupling can be amplified in the MSSM. Some theorists believe this is supporting evidence for the MSSM.

The quasi-infrared fixed point has subsequently formed the basis of top quark condensation theories of electroweak symmetry breaking in which the Higgs boson is composite at extremely short distance scales, composed of a pair of top and antitop quarks.

See also

References

  1. 1 2 CMS Collaboration (2016). "Measurement of the top quark mass using proton-proton data at sqrt(s) = 7 and 8 TeV". arXiv:1509.04044Freely accessible [hep-ex].
  2. ↑ S. Willenbrock (2003). "The Standard Model and the Top Quark". In H.B Prosper; B. Danilov. Techniques and Concepts of High-Energy Physics XII. NATO Science Series. 123. Kluwer Academic. pp. 1–41. arXiv:hep-ph/0211067v3Freely accessible. ISBN 1-4020-1590-9.
  3. 1 2 A. Quadt (2006). "Top quark physics at hadron colliders". European Physical Journal C. 48 (3): 835–1000. Bibcode:2006EPJC...48..835Q. doi:10.1140/epjc/s2006-02631-6.
  4. 1 2 M. Kobayashi; T. Maskawa (1973). "CP-Violation in the Renormalizable Theory of Weak Interaction". Progress of Theoretical Physics. 49 (2): 652. Bibcode:1973PThPh..49..652K. doi:10.1143/PTP.49.652.
  5. 1 2 F. Abe et al. (CDF Collaboration) (1995). "Observation of Top Quark Production in
    p

    p
     Collisions with the Collider Detector at Fermilab". Physical Review Letters. 74 (14): 2626–2631. Bibcode:1995PhRvL..74.2626A. doi:10.1103/PhysRevLett.74.2626. PMID 10057978.
  6. 1 2 S. Abachi et al. (DØ Collaboration) (1995). "Search for High Mass Top Quark Production in
    p

    p
     Collisions at √s = 1.8 TeV". Physical Review Letters. 74 (13): 2422–2426. Bibcode:1995PhRvL..74.2422A. doi:10.1103/PhysRevLett.74.2422.
  7. ↑ "2008 Nobel Prize in Physics". The Nobel Foundation. 2008. Retrieved 2009-09-11.
  8. ↑ H. Harari (1975). "A new quark model for hadrons". Physics Letters B. 57 (3): 265. Bibcode:1975PhLB...57..265H. doi:10.1016/0370-2693(75)90072-6.
  9. ↑ K.W. Staley (2004). The Evidence for the Top Quark. Cambridge University Press. pp. 31–33. ISBN 978-0-521-82710-2.
  10. ↑ D.H. Perkins (2000). Introduction to high energy physics. Cambridge University Press. p. 8. ISBN 0-521-62196-8.
  11. ↑ F. Close (2006). The New Cosmic Onion. CRC Press. p. 133. ISBN 1-58488-798-2.
  12. ↑ S.L. Glashow; J. Iliopoulous; L. Maiani (1970). "Weak Interactions with Lepton–Hadron Symmetry". Physical Review D. 2 (7): 1285–1292. Bibcode:1970PhRvD...2.1285G. doi:10.1103/PhysRevD.2.1285.
  13. ↑ A. Pickering (1999). Constructing Quarks: A Sociological History of Particle Physics. University of Chicago Press. pp. 253–254. ISBN 978-0-226-66799-7.
  14. ↑ M.L. Perl; et al. (1975). "Evidence for Anomalous Lepton Production in
    e+

    e−
     Annihilation". Physical Review Letters. 35 (22): 1489. Bibcode:1975PhRvL..35.1489P. doi:10.1103/PhysRevLett.35.1489.
  15. ↑ "Discoveries at Fermilab – Discovery of the Bottom Quark" (Press release). Fermilab. 7 August 1977. Retrieved 2009-07-24.
  16. ↑ L.M. Lederman (2005). "Logbook: Bottom Quark". Symmetry Magazine. 2 (8).
  17. ↑ S.W. Herb; et al. (1977). "Observation of a Dimuon Resonance at 9.5 GeV in 400-GeV Proton-Nucleus Collisions". Physical Review Letters. 39 (5): 252. Bibcode:1977PhRvL..39..252H. doi:10.1103/PhysRevLett.39.252.
  18. 1 2 3 T.M. Liss; P.L. Tipton (1997). "The Discovery of the Top Quark" (PDF). Scientific American: 54–59.
  19. ↑ The Discovery of the Top Quark, Tony M. Liss and Paul L. Tipton
  20. ↑ "The Nobel Prize in Physics 1999". The Nobel Foundation. Retrieved 2009-09-10.
  21. ↑ "The Nobel Prize in Physics 1999, Press Release" (Press release). The Nobel Foundation. 12 October 1999. Retrieved 2009-09-10.
  22. ↑ D. Chakraborty (DØ and CDF collaborations) (2002). Top quark and W/Z results from the Tevatron (PDF). Rencontres de Moriond. p. 26.
  23. ↑ V.M. Abazov et al. (DØ Collaboration) (2007). "Experimental discrimination between charge 2e/3 top quark and charge 4e/3 exotic quark production scenarios". Physical Review Letters. 98 (4): 041801. arXiv:hep-ex/0608044Freely accessible. Bibcode:2007PhRvL..98d1801A. doi:10.1103/PhysRevLett.98.041801. PMID 17358756.
  24. 1 2 V.M. Abazov et al. (DØ Collaboration) (2009). "Observation of Single Top Quark Production". Physical Review Letters. 103 (9): 092001. arXiv:0903.0850Freely accessible. Bibcode:2009PhRvL.103i2001A. doi:10.1103/PhysRevLett.103.092001. PMID 19792787.
  25. ↑ V.M. Abazov et al. (DØ Collaboration) (2007). "Evidence for production of single top quarks and first direct measurement of |Vtb|". Physical Review Letters. 98 (18): 181802. arXiv:hep-ex/0612052Freely accessible. Bibcode:2007PhRvL..98r1802A. doi:10.1103/PhysRevLett.98.181802. PMID 17501561.
  26. ↑ T. Aaltonen et al. (CDF Collaboration) (2009). "First Observation of Electroweak Single Top Quark Production". Physical Review Letters. 103 (9): 092002. arXiv:0903.0885Freely accessible. Bibcode:2009PhRvL.103i2002A. doi:10.1103/PhysRevLett.103.092002.
  27. 1 2 J. Beringer et al. (Particle Data Group) (2012). "PDGLive Particle Summary 'Quarks (u, d, s, c, b, t, b', t', Free)'" (PDF). Particle Data Group. Retrieved 2013-07-23.
  28. ↑ V.M. Abazov et al. (DØ Collaboration) (2008). "Simultaneous measurement of the ratio B(t→Wb)/B(t→Wq) and the top-quark pair production cross section with the DØ detector at √s = 1.96 TeV". Physical Review Letters. 100 (19): 192003. arXiv:0801.1326Freely accessible. Bibcode:2008PhRvL.100s2003A. doi:10.1103/PhysRevLett.100.192003.
  29. ↑ S. Chekanov et al. (ZEUS Collaboration) (2003). "Search for single-top production in ep collisions at HERA". Physics Letters B. 559 (3–4): 153. arXiv:hep-ex/0302010Freely accessible. Bibcode:2003PhLB..559..153Z. doi:10.1016/S0370-2693(03)00333-2.

Further reading

This article is issued from Wikipedia - version of the 11/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.