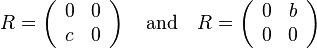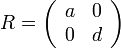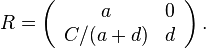Square root of a 2 by 2 matrix
A square root of a 2 by 2 matrix M is another 2 by 2 matrix R such that M = R2, where R2 stands for the matrix product of R with itself. In general there can be no, two, four or even an infinitude of square root matrices. In many cases such a matrix R can be obtained by an explicit formula.
A 2 × 2 matrix with two distinct nonzero eigenvalues has four square roots. A positive-definite matrix has precisely one positive-definite square root.
Square roots of a matrix of any dimension come in pairs: If R is a square root of M, then –R is also a square root of M, since (–R)(–R) = (–1)(–1)(RR) = R2 = M.
One formula
where A, B, C, and D may be real or complex numbers. Furthermore, let τ = A + D be the trace of M, and δ = AD - BC be its determinant. Let s be such that s2 = δ, and t be such that t2 = τ + 2s. That is,
Then, if t ≠ 0, a square root of M is
Indeed, the square of R is
Note that R may have complex entries even if M is a real matrix; this will be the case, in particular, if the determinant δ is negative. Also, note that R is positive when s>0 and t>0.
Special cases of the formula
If M is an idempotent matrix, meaning that MM = M, then if it is not the identity matrix its determinant is zero, and its trace equals its rank which (excluding the zero matrix) is 1. Then the above formula has s = 0 and 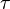 = 1, giving M and -M as two square roots of M.
= 1, giving M and -M as two square roots of M.
In general, the formula above will provide four distinct square roots R, one for each choice of signs for s and t. If the determinant δ is zero but the trace τ is nonzero, the formula will give only two distinct solutions. It also gives only two distinct solutions if δ is nonzero and τ2 = 4δ (the case of duplicate eigenvalues), in which case one of the choices for s will make the denominator t be zero.
The formula above fails completely if δ and τ are both zero; that is, if D = −A and A2 = −BC, so that both the trace and the determinant of the matrix are zero. In this case, if M is the null matrix (with A = B = C = D = 0), then the null matrix is also a square root of M, as are
for any real or complex values of b and c. Otherwise M has no square root.
Simpler formulas for special matrices
Diagonal matrix
If M is diagonal (that is, B = C = 0), one can use the simplified formula
where a = ±√A and d = ±√D; which, depending on the sign choices, gives four, two, or one distinct matrices, if none of, only one of, or both A and D are zero, respectively.
Identity matrix
Because it has duplicate eigenvalues, the 2×2 identity matrix 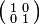 has infinitely many symmetric rational square roots given by
has infinitely many symmetric rational square roots given by
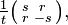
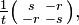
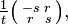
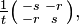
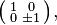 and
and 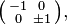
where (r, s, t) is any Pythagorean triple—that is, any set of positive integers such that 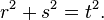 [3] In addition, any non-integer, irrational, or complex values of r, s, t satisfying
[3] In addition, any non-integer, irrational, or complex values of r, s, t satisfying 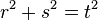 give square root matrices. The identity matrix also has infinitely many non-symmetric square roots.
give square root matrices. The identity matrix also has infinitely many non-symmetric square roots.
Matrix with one off-diagonal zero
If B is zero but A and D are not both zero, one can use
This formula will provide two solutions if A = D, and four otherwise. A similar formula can be used when C is zero but A and D are not both zero.
References
- ↑ Levinger, Bernard W.. 1980. “The Square Root of a 2 × 2 Matrix”. Mathematics Magazine 53 (4). Mathematical Association of America: 222–24. doi:10.2307/2689616.
- ↑ P. C. Somayya (1997), Root of a 2x2 Matrix, The Mathematics Education, Vol.. XXXI, no. 1. Siwan, Bihar State. INDIA
- ↑ Mitchell, Douglas W. "Using Pythagorean triples to generate square roots of I2". The Mathematical Gazette 87, November 2003, 499-500.
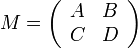

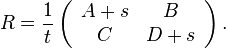
![\begin{array}{rcl}
R^2
&=&
\displaystyle \frac{1}{t^2}
\left( \begin{array}{cc} (A + s)^2 + B C & (A + s)B + B(D + s) \\ C(A + s) + (D + s)C & (D + s)^2 + B C \end{array}\right)\\[3ex]
{}
&=&
\displaystyle \frac{1}{A + D + 2 s}
\left( \begin{array}{cc} A(A + D + 2s) & (A + D + 2s)B \\ C(A + D + 2 s) & D(A + D + 2 s) \end{array}\right) \;=\;
M.
\end{array}](../I/m/0a86ad85ebf3fccab1a13fbb38dab016.png)