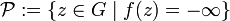Pluripolar set
In mathematics, in the area of potential theory, a pluripolar set is the analog of a polar set for plurisubharmonic functions.
Definition
Let 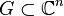 and let
and let 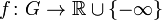 be a plurisubharmonic function which is not identically
be a plurisubharmonic function which is not identically 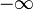 . The set
. The set
is called a complete pluripolar set. A pluripolar set is any subset of a complete pluripolar set. Pluripolar sets are of Hausdorff dimension at most  and have zero Lebesgue measure.[1]
and have zero Lebesgue measure.[1]
If 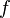 is a holomorphic function then
is a holomorphic function then 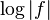 is a plurisubharmonic function. The zero set of
is a plurisubharmonic function. The zero set of 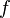 is then a pluripolar set.
is then a pluripolar set.
See also
References
- Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.
This article incorporates material from pluripolar set on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This article is issued from Wikipedia - version of the 1/5/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.