NAND logic

Because the NAND function has functional completeness all logic systems can be converted into NAND gates. This is also true of NOR gates. In principle, any combinatorial logic function can be realized with enough NAND gates.

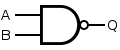
NAND

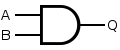
A NAND gate is an inverted AND gate. It has the following truth table:

Q = NOT( A AND B ) Truth Table Input A Input B Output Q 0 0 1 0 1 1 1 0 1 1 1 0

NOT

A NOT gate is made by joining the inputs of a NAND gate together. Since a NAND gate is equivalent to an AND gate followed by a NOT gate, joining the inputs of a NAND gate leaves only the NOT gate.

Desired NOT Gate	NAND Construction
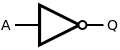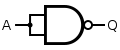Q = NOT( A )	= NOT( A AND A )
Truth Table Input A Output Q 0 1 1 0

AND

An AND gate is made by following a NAND gate with a NOT gate as shown below. This gives a NOT NAND, i.e. AND.

Desired AND Gate	NAND Construction
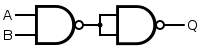Q = A AND B	= NOT[ NOT( A AND B ) AND NOT( A AND B ) ]
Truth Table Input A Input B Output Q 0 0 0 0 1 0 1 0 0 1 1 1

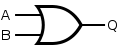
OR

If the truth table for a NAND gate is examined or by applying De Morgan's Laws, it can be seen that if any of the inputs are 0, then the output will be 1. To be an OR gate, however, the output must be 1 if any input is 1. Therefore, if the inputs are inverted, any high input will trigger a high output.

Desired OR Gate	NAND Construction
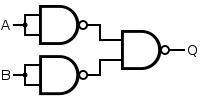Q = A OR B	= NOT[ NOT( A AND A ) AND NOT( B AND B )]
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 1

NOR

A NOR gate is simply an inverted OR gate. Output is high when neither input A nor input B is high:

Desired NOR Gate	NAND Construction
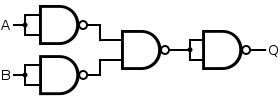Q = NOT( A OR B )	= NOT{ NOT[ NOT( A AND A ) AND NOT( B AND B )] AND NOT[ NOT( A AND A ) AND NOT( B AND B )] }
Truth Table Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 0

XOR

An XOR gate is constructed similarly to an OR gate, except with an additional NAND gate inserted such that if both inputs are high, the inputs to the final NAND gate will also be high, and the output will be low.

Desired XOR Gate	NAND Construction
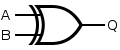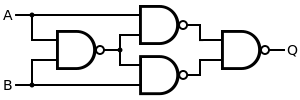Q = A XOR B	= NOT{ NOT[ A AND NOT( A AND B ) ] AND NOT[ B AND NOT( A AND B ) ] }
Truth Table Input A Input B Output Q 0 0 0 0 1 1 1 0 1 1 1 0

XNOR

An XNOR gate is simply an XOR gate with an inverted output:

Desired XNOR Gate	NAND Construction
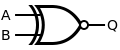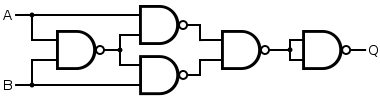Q = NOT( A XOR B)	= NOT( NOT{ NOT[ A AND NOT( A AND B ) ] AND NOT[ B AND NOT( A AND B ) ] } AND NOT{ NOT[ A AND NOT( A AND B ) ] AND NOT[ B AND NOT( A AND B ) ] } )
Truth Table Input A Input B Output Q 0 0 1 0 1 0 1 0 0 1 1 1

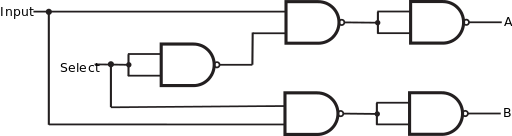
MUX

A multiplexer or a MUX gate is a three-input gate that uses one of the inputs, called "selection bits", to select and output one of the other two inputs, called "data bits".^[1]

DEMUX

A demultiplexer performs the opposite function of a multiplexer: It takes a single input and channels it to one of two possible outputs according to a selector bit that specifies which output to choose.^[1]

See also

• NOR logic. Like NAND gates, NOR gates are also universal gates.
• Functional Completeness

External links

• TTL NAND and AND gates - All About Circuits
• Steps to Derive XOR from NAND gate.
• NAND Gate, Demonstrate an interactive simulation of the NAND Gate circuit created with Teahlab's simulator.

References

1. 1 2 Nisan, N. & Schocken, S., 2005. In: From NAND to Tetris: Building a Modern Computer from First Principles. s.l.:The MIT Press, p. 20. Available at: http://www.nand2tetris.org/chapters/chapter%2001.pdf

Lancaster, Don (1974). TTL Cookbook (1st ed.). Indianapolis, IN: Howard W Sams. pp. 126–135. ISBN 0-672-21035-5.