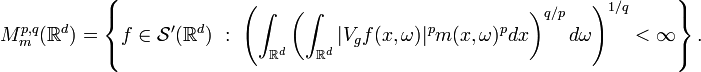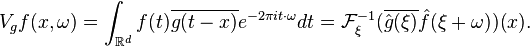Modulation space

Modulation spaces^[1] are a family of Banach spaces defined by the behavior of the short-time Fourier transform with respect to a test function from the Schwartz space. They were originally proposed by Hans Georg Feichtinger and are recognized to be the right kind of function spaces for time-frequency analysis. Feichtinger's algebra, while originally introduced as a new Segal algebra,^[2] is identical to a certain modulation space and has become a widely used space of test functions for time-frequency analysis.

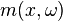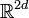Modulation spaces are defined as follows. For $1\leq p,q \leq \infty$ , a non-negative function $m(x,\omega)$ on $\mathbb{R}^{2d}$ and a test function 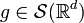$g \in \mathcal{S}(\mathbb{R}^d)$ , the modulation space 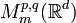$M^{p,q}_m(\mathbb{R}^d)$ is defined by

M^{p,q}_m(\mathbb{R}^d) = \left\{ f\in \mathcal{S}'(\mathbb{R}^d)\ :\ \left(\int_{\mathbb{R}^d}\left(\int_{\mathbb{R}^d} |V_gf(x,\omega)|^p m(x,\omega)^p dx\right)^{q/p} d\omega\right)^{1/q} < \infty\right\}.

In the above equation, 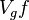$V_gf$ denotes the short-time Fourier transform of 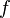$f$ with respect to 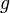$g$ evaluated at 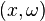$(x,\omega)$ , namely

V_gf(x,\omega)=\int_{\mathbb{R}^d}f(t)\overline{g(t-x)}e^{-2\pi it\cdot \omega}dt=\mathcal{F}^{-1}_{\xi}(\overline{\hat{g}(\xi)}\hat{f}(\xi+\omega))(x).

In other words, 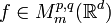$f\in M^{p,q}_m(\mathbb{R}^d)$ is equivalent to 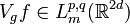$V_gf\in L^{p,q}_m(\mathbb{R}^{2d})$ . The space 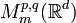$M^{p,q}_m(\mathbb{R}^d)$ is the same, independent of the test function 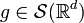$g \in \mathcal{S}(\mathbb{R}^d)$ chosen. The canonical choice is a Gaussian.

We also have a Besov-type definition of modulation spaces as follows.^[3]

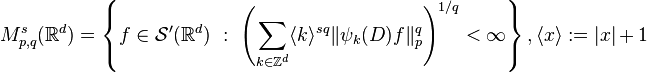M^s_{p,q}(\mathbb{R}^d) = \left\{ f\in \mathcal{S}'(\mathbb{R}^d)\ :\ \left(\sum_{k\in\mathbb{Z}^d} \langle k \rangle^{sq} \|\psi_k(D)f\|_p^q\right)^{1/q} < \infty\right\}, \langle x\rangle:=|x|+1

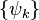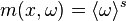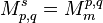where $\{\psi_k\}$ is a suitable unity partition. If $m(x,\omega)=\langle \omega\rangle^s$ , then $M^s_{p,q}=M^{p,q}_m$ .

Feichtinger's algebra

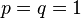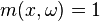For $p=q=1$ and $m(x,\omega) = 1$ , the modulation space 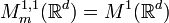$M^{1,1}_m(\mathbb{R}^d) = M^1(\mathbb{R}^d)$ is known by the name Feichtinger's algebra and often denoted by 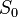$S_0$ for being the minimal Segal algebra invariant under time-frequency shifts, i.e. combined translation and modulation operators. 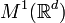$M^1(\mathbb{R}^d)$ is a Banach space embedded in 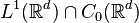$L^1(\mathbb{R}^d) \cap C_0(\mathbb{R}^d)$ , and is invariant under the Fourier transform. It is for these and more properties that 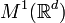$M^1(\mathbb{R}^d)$ is a natural choice of test function space for time-frequency analysis. 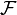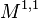Fourier transform $\mathcal{F}$ is an automorphism on $M^{1,1}$ .

References

↑ Foundations of Time-Frequency Analysis by Karlheinz Gröchenig
↑ H. Feichtinger. "On a new Segal algebra" Monatsh. Math. 92:269–289, 1981.
↑ B.X. Wang, Z.H. Huo, C.C. Hao, and Z.H. Guo. Harmonic Analysis Method for Nonlinear Evolution Equations. World Scientific, 2011.

This article is issued from Wikipedia - version of the 6/28/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.