Light-cone coordinates

In special relativity, light-cone coordinates is a special coordinate system where two of the coordinates, x⁺ and x⁻ are null coordinates and all the other coordinates are spatial. Call them 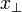$x_\perp$ .

Assume we're working with a (d,1) Lorentzian signature.

Instead of the standard coordinate system (using Einstein notation)

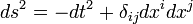ds^2=-dt^2+\delta_{ij}dx^i dx^j

with 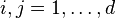$i,j=1,\dots,d$ we have

ds^2=-2dx^+dx^- + \delta_{ij}dx^i dx^j

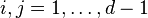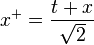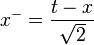with $i,j=1,\dots,d-1$ , $x^+=\frac{t+x}{\sqrt{2}}$ and $x^-=\frac{t-x}{\sqrt{2}}$ .

Both x⁺ and x⁻ can act as "time" coordinates.

One nice thing about light cone coordinates is that the causal structure is partially included into the coordinate system itself.

A boost in the tx plane shows up as 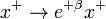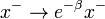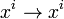$x^+ \to e^{+\beta}x^+$ , $x^- \to e^{-\beta}x^-$ , $x^i \to x^i$ . A rotation in the ij-plane only affects 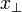$x_\perp$ . The parabolic transformations show up as 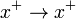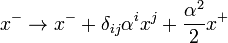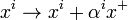$x^+ \to x^+$ , $x^- \to x^- + \delta_{ij}\alpha^i x^j + \frac{\alpha^2}{2} x^+$ , $x^i \to x^i + \alpha^i x^+$ . 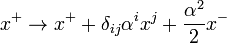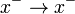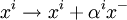Another set of parabolic transformations show up as $x^+ \to x^+ + \delta_{ij}\alpha^i x^j + \frac{\alpha^2}{2} x^-$ , $x^- \to x^-$ and $x^i \to x^i + \alpha^i x^-$ .

Light cone coordinates can also be generalized to curved spacetime in general relativity. Sometimes, calculations simplify using light cone coordinates. See Newman–Penrose formalism.

Light cone coordinates are sometimes used to describe relativistic collisions, especially if the relative velocity is very close to the speed of light. It's also used in the light cone gauge of string theory.

Light-cone coordinates

See also