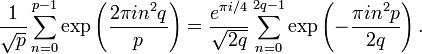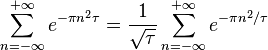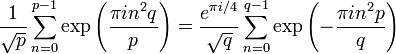Landsberg–Schaar relation
In number theory and harmonic analysis, the Landsberg–Schaar relation (or identity) is the following equation, which is valid for arbitrary positive integers p and q:
Although both sides are mere finite sums, no proof by entirely finite methods has yet been found. The standard way to prove it[1] is to put 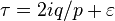 , where
, where 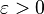 in this identity due to Jacobi (which is essentially just a special case of the Poisson summation formula in classical harmonic analysis):
in this identity due to Jacobi (which is essentially just a special case of the Poisson summation formula in classical harmonic analysis):
and then let 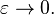
If we let q = 1, the identity reduces to a formula for the quadratic Gauss sum modulo p.
The Landsberg–Schaar identity can be rephrased more symmetrically as
provided that we add the hypothesis that pq is an even number.
References
- ↑ H. Dym and H.P. McKean. Fourier Series and Integrals. Academic Press, 1972.
This article is issued from Wikipedia - version of the 8/17/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.