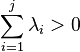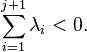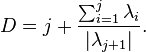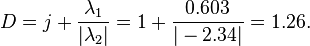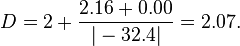Kaplan–Yorke conjecture
In applied mathematics, the Kaplan–Yorke conjecture concerns the dimension of an attractor, using Lyapunov exponents.[1][2] By arranging the Lyapunov exponents in order from largest to smallest 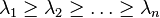 , let j be the index for which
, let j be the index for which
and
Then the conjecture is that the dimension of the attractor is
Examples
Especially for chaotic systems, the Kaplan–Yorke conjecture is a useful tool in order to determine the fractal dimension of the corresponding attractor.[3]
- The Hénon map with parameters a = 1.4 and b = 0.3 has the ordered Lyapunov exponents
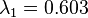 and
and 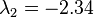 . In this case, we find j = 1 and the dimension formula reduces to
. In this case, we find j = 1 and the dimension formula reduces to
- The Lorenz system shows chaotic behavior at the parameter values
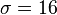 ,
,  and
and 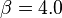 . The resulting Lyapunov exponents are {2.16, 0.00, -32.4}. Noting that j = 2, we find
. The resulting Lyapunov exponents are {2.16, 0.00, -32.4}. Noting that j = 2, we find
References
- ↑ J. Kaplan and J. Yorke, "Chaotic behavior of multidimensional difference equations," in: Functional Differential Equations and the Approximation of Fixed Points, Lecture Notes in Mathematics, vol. 730, H.O. Peitgen and H.O. Walther, eds. (Springer, Berlin), p. 228.
- ↑ P. Frederickson, J. Kaplan, E. Yorke and J. Yorke, "The Lyapunov Dimension of Strange Attractors," J. Diff. Eqs. 49 (1983) 185.
- ↑ A. Wolf, A. Swift, B. Jack, H. L. Swinney and J.A. Vastano "Determining Lyapunov Exponents from a Time Series," Physica 16D, 1985, 16, pp. 285–317.
This article is issued from Wikipedia - version of the 3/9/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.