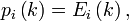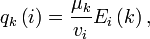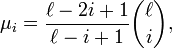Johnson scheme
In mathematics, the Johnson scheme, named after Selmer M. Johnson, is also known as the triangular association scheme. It consists of the set of all binary vectors X of length ℓ and weight n, such that 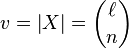 .[1][2][3] Two vectors x, y ∈ X are called ith associates if dist(x, y) = 2i for i = 0, 1, ..., n. The eigenvalues are given by
.[1][2][3] Two vectors x, y ∈ X are called ith associates if dist(x, y) = 2i for i = 0, 1, ..., n. The eigenvalues are given by
where
and Ek(x) is an Eberlein polynomial defined by
References
- ↑ P. Delsarte and V. I. Levenshtein, “Association schemes and coding theory,“ IEEE Trans. Inform. Theory, vol. 44, no. 6, pp. 2477–2504, 1998.
- ↑ P. Camion, "Codes and Association Schemes: Basic Properties of Association Schemes Relevant to Coding," in Handbook of Coding Theory, V. S. Pless and W. C. Huffman, Eds., Elsevier, The Netherlands, 1998.
- ↑ F. J. MacWilliams and N. J. A. Sloane, The Theory of Error-Correcting Codes, Elsevier, New York, 1978.
This article is issued from Wikipedia - version of the 1/7/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.