Hilbert's fourth problem
In mathematics, Hilbert's fourth problem in the 1900 Hilbert problems is a foundational question in geometry. In one statement derived from the original, it was to find geometries whose axioms are closest to those of Euclidean geometry if the ordering and incidence axioms are retained, the congruence axioms weakened, and the equivalent of the parallel postulate omitted. The original statement of Hilbert has been judged too vague to admit a definitive answer. Nevertheless a solution was found with The famous German mathematician Georg Hamel being the first who tried to solve the problem but a recognized independent solution for dimension 2 and 3 is considered to be given by Rouben V. Ambartzumian.
Original statement
Hilbert discusses the existence of non-Euclidean geometry and non-Archimedean geometry, as well as the idea that a 'straight line' is defined as the shortest path between two points. He mentions how congruence of triangles is necessary for Euclid's proof that a straight line in the plane is the shortest distance between two points. He summarizes as follows:
The theorem of the straight line as the shortest distance between two points and the essentially equivalent theorem of Euclid about the sides of a triangle, play an important part not only in number theory but also in the theory of surfaces and in the calculus of variations. For this reason, and because I believe that the thorough investigation of the conditions for the validity of this theorem will throw a new light upon the idea of distance, as well as upon other elementary ideas, e. g., upon the idea of the plane, and the possibility of its definition by means of the idea of the straight line, the construction and systematic treatment of the geometries here possible seem to me desirable.[1]
Interpretations
One popular interpretation of this problem is that it is asking for all metrics on convex portions of the plane where the geodesics are straight Euclidean lines. [2]
Hilbert's Fourth Problem in dimension 3
One of the solutions of Hilbert's Fourth problem in dimension 2 was obtained[3] in 1976 by Rouben V. Ambartzumian in the framework of his theory of Combinatorial Integral Geometry[4] by application of measure continuation starting from "Buffonic" valuations in the space of lines in the plane. Recently (2014) an attempt was made by Rouben V. Ambartzumian to apply the same techniques starting from similar valuations that live in the space of planes in 3 dimensional Euclidean space. The paper[5] puts forward the concept of wedge metrics and formulates some conditions for a wedge metric to generate a measure in the space of planes. The definition of a wedge metrics is based on certain tetrahedral inequalities of combinatorial nature. The latter inequalities replace the usual triangle inequality.
Examples
Gnomonic projection
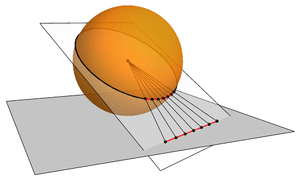
A gnomonic map projection of the sphere displays all great circles as straight lines, resulting in any line segment on a gnomonic map showing the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the earth passes through the point on the surface and then on to the plane.
This projection allows one to give a spherical metric to the portion of the plane it maps onto.
Klein disk model

In geometry, the Klein disk model is a model of 2-dimensional hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with endpoints on the boundary circle.
References
- ↑ Hilbert, David, "Mathematische Probleme" Göttinger Nachrichten, (1900), pp. 253–297, and in Archiv der Mathematik und Physik, (3) 1 (1901), 44–63 and 213–237. Published in English translation by Dr. Maby Winton Newson, Bulletin of the American Mathematical Society 8 (1902), 437–479 doi:10.1090/S0002-9904-1902-00923-3 . [A fuller title of the journal Göttinger Nachrichten is Nachrichten von der Königl. Gesellschaft der Wiss. zu Göttingen.]
- ↑ Paiva, JC Álvarez. "Hilbert’s fourth problem in two dimensions." MASS selecta (2003): 165–183.
- ↑ R. V. Ambartzumian, A note on pseudo-metrics on the plane, Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1976, Volume 37, Issue 2, pp 145–155
- ↑ by R. V. Ambartzumian, Combinatorial integral geometry with applications to mathematical stereology, John Wiley & Sons, 1982, ISBN 0-4712-7977-3
- ↑ R. V. Ambartzumian, Remarks on Combinatorics of Planes in Euclidean Three Dimensions, SOP Transactions on Applied Mathematics, Volume 1, Number 2, pp. 29–43, 2014.
Further reading
- Busemann, Herbert (1976). "Problem IV. Desarguesian spaces". In Browder, Felix E. Mathematical Developments Arising from Hilbert Problems. Proceedings of Symposia in Pure Mathematics. XXVIII. American Mathematical Society. pp. 131–141. ISBN 0-8218-1428-1. Zbl 0352.50010.
- Papadopoulos, Athanase. "Hilbert's fourth problem". Handbook of Hilbert geometry (A. Papadopoulos and M. Troyanov, ed.). IRMA Lectures in Mathematics and Theoretical Physics. 22 (2014). European Mathematical Society. pp. 391–432. ISBN 978-3-03719-147-7.