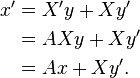Green's matrix
In mathematics, and in particular ordinary differential equations, a Green's matrix helps to determine a particular solution to a first-order inhomogeneous linear system of ODEs. The concept is named after George Green.
For instance, consider 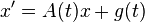 where
where 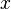 is a vector and
is a vector and 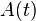 is an
is an 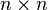 matrix function of
matrix function of 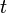 , which is continuous for
, which is continuous for 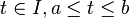 , where
, where 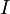 is some interval.
is some interval.
Now let 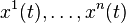 be
be 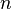 linearly independent solutions to the homogeneous equation
linearly independent solutions to the homogeneous equation 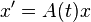 and arrange them in columns to form a fundamental matrix:
and arrange them in columns to form a fundamental matrix:
Now 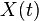 is an
is an 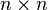 matrix solution of
matrix solution of 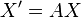 .
.
This fundamental matrix will provide the homogeneous solution, and if added to a particular solution will give the general solution to the inhomogeneous equation.
Let 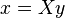 be the general solution. Now,
be the general solution. Now,
This implies 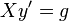 or
or 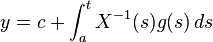 where
where  is an arbitrary constant vector.
is an arbitrary constant vector.
Now the general solution is 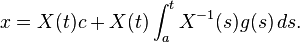
The first term is the homogeneous solution and the second term is the particular solution.
Now define the Green's matrix 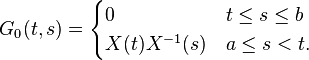
The particular solution can now be written 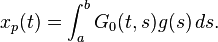
External links
- An example of solving an inhomogeneous system of linear ODEs and finding a Green's matrix from www.exampleproblems.com.
![X(t) = \left[ x^1(t),\ldots,x^n(t) \right].\,](../I/m/d3714f7262a061618d32f8a7e2e44b1a.png)