Gomory–Hu tree
In combinatorial optimization, the Gomory–Hu tree[1] of an undirected graph with capacities is a weighted tree that represents the minimum s-t cuts for all s-t pairs in the graph. The Gomory–Hu tree can be constructed in | V | − 1 maximum flow computations.
Definition
Let G = ((VG, EG), c) be an undirected graph with c(u,v) being the capacity of the edge (u,v) respectively.
- Denote the minimum capacity of an s-t cut by λst for each s, t ∈ VG.
- Let T = (VT,ET) be a tree with VT = VG, denote the set of edges in an s-t path by Pst for each s,t ∈ VT.
Then T is said to be a Gomory–Hu tree of G if
- λst = mine∈Pst c(Se, Te) for all s, t ∈ VG,
where
- Se and Te are the two connected components of T∖{e} in the sense that (Se, Te) form a s-t cut in G, and
- c(Se, Te) is the capacity of the cut in G.
Algorithm
Gomory–Hu Algorithm
- Input: A weighted undirected graph G = ((VG, EG), c)
- Output: A Gomory–Hu Tree T = (VT, ET).
- 1. Set VT = {VG} and ET = ∅.
- 2. Choose some X∈VT with | X | ≥ 2 if such X exists. Otherwise, go to step 6.
- 3. For each connected component C = (VC, EC) in T∖X. Let SC = ∪vT∈VC vT. Let S = { SC | C is a connected component in T∖X}.
- Contract the components to form G' = ((VG', EG'), c'), where
- VG' = X ∪ S.
- EG' = EG|X×X ∪ {(u, SC) ∈ X×S | (u,v)∈EG for some v∈SC}.
- c' : VG'×VG'→R+ is the capacity function defined as,
- if (u,SC)∈EG|X×S, c'(u,SC) = Σv∈SC:(u,v)∈EGc(u,v),
- c'(u,v) = c(u,v) otherwise.
- 4. Choose two vertices s, t ∈ X and find a minimum s-t cut (A',B') in G'.
- Set A = (∪SC∈A'∩S SC) ∪ (A' ∩ X) and B = (∪SC∈B'∩S SC) ∪ (B' ∩ X).
- 5. Set VT = (VT∖X) ∪ {A ∩ X, B ∩ X}.
- For each e = (X, Y) ∈ ET do
- If Y⊂A, set e' = (A ∩ X, Y), else set e' = (B ∩ X, Y).
- Set ET = (ET∖{e}) ∪ {e'} and w(e') = w(e).
- Set ET = ET ∪ {(A∩X, B∩X)}.
- Set w((A∩X, B∩X)) = c'(A', B').
- Go to step 2.
- 6. Replace each {v} ∈ VT by v and each ({u},{v}) ∈ ET by (u,v). Output T.
Analysis
Using the submodular property of the capacity function c, one has
- c(X) + c(Y) ≥ c(X ∩ Y) + c(X ∪ Y).
Then it can be shown that the minimum s-t cut in G' is also a minimum s-t cut in G for any s, t ∈ X.
To show that for all (P, Q) ∈ ET, w(P,Q) = λpq for some p ∈ P, q ∈ Q throughout the algorithm, one makes use of the following Lemma,
- For any i, j, k in VG, λik ≥ min(λij, λjk).
The Lemma can be used again repeatedly to show that the output T satisfies the properties of a Gomory–Hu Tree.
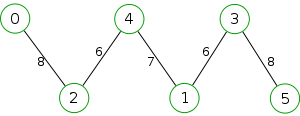
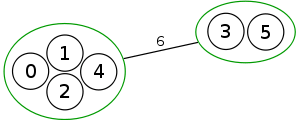
Example
The following is a simulation of the Gomory–Hu's algorithm, where
- green circles are vertices of T.
- red and blue circles are the vertices in G'.
- grey vertices are the chosen s and t.
- red and blue coloring represents the s-t cut.
- dashed edges are the s-t cut-set.
- A is the set of vertices circled in red and B is the set of vertices circled in blue.
| G' | T | |
|---|---|---|
 |
 | |
| ||
| 1. | 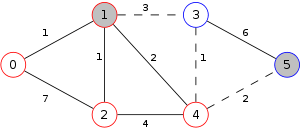 |
 |
| ||
| 2. | 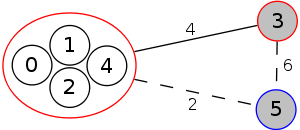 |
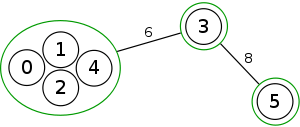 |
| ||
| 3. | 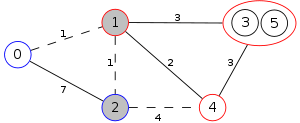 |
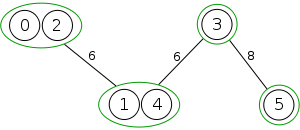 |
| ||
| 4. |  |
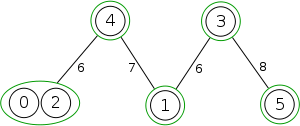 |
| ||
| 5. | 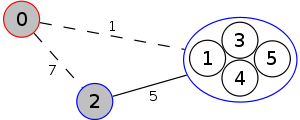 |
 |
| ||
| 6. |
| |
| ||
Implementations: Sequential and Parallel
Gusfield's algorithm can be used to find a Gomory–Hu tree without any vertex contraction in the same running time-complexity, which simplifies the implementation of constructing a Gomory–Hu Tree.
Andrew V. Goldberg and K. Tsioutsiouliklis implemented the Gomory-Hu algorithm and Gusfield algorithm. Experimental results comparing these algorithms are reported in[2] Source code is available here.
Cohen et al.[3] reports results on two parallel implementations of Gusfield's algorithm using OpenMP and MPI, respectively. Source code of these implementations is available here: Parallel Cut Tree Algorithms Page. (broken link)
History
The Gomory–Hu tree was introduced by R. E. Gomory and T. C. Hu in 1961.
Related concepts
In planar graphs, the Gomory–Hu tree is dual to the minimum weight cycle basis, in the sense that the cuts of the Gomory–Hu tree are dual to a collection of cycles in the dual graph that form a minimum-weight cycle basis.[4]
See also
References
- ↑ Gomory, R. E.; Hu, T. C. (1961). "Multi-terminal network flows". Journal of the Society for Industrial and Applied Mathematics. 9.
- ↑ Goldberg, A. V.; Tsioutsiouliklis, K. (2001). "Cut Tree Algorithms: An Experimental Study". Journal of Algorithms. 38 (1): 51–83. doi:10.1006/jagm.2000.1136.
- ↑ Cohen, J.; L. A. Rodrigues; F. Silva; R. Carmo; A. Guedes; E. P. Duarte Jr. (2011). "Parallel Implementations of Gusfield's Cut Tree Algorithm". Lecture Notes in Computer Science (LNCS). 7016. Springer (11th International Conference Algorithms and Architectures for Parallel Processing (ICA3PP)). ISSN 0302-9743.
- ↑ Hartvigsen, D.; Mardon, R. (1994). "The all-pairs min cut problem and the minimum cycle basis problem on planar graphs". SIAM J. on Discrete Math. 7 (3): 403–418. doi:10.1137/S0895480190177042..
- Dan Gusfield (1990). "Very Simple Methods for All Pairs Network Flow Analysis". SIAM J. Comput. 19 (1): 143–155. doi:10.1137/0219009.
- B. H. Korte, Jens Vygen (2008). "8.6 Gomory–Hu Trees". Combinatorial Optimization: Theory and Algorithms (Algorithms and Combinatorics, 21). Springer Berlin Heidelberg. pp. 180–186. ISBN 978-3-540-71844-4.