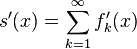Fubini's theorem on differentiation
In mathematics, Fubini's theorem on differentiation, named after Guido Fubini, is a result in real analysis concerning the differentiation of series of monotonic functions. It can be proven by using Fatou's lemma and the properties of null sets.[1]
Statement
Assume 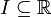 is an interval and that for every natural number k,
is an interval and that for every natural number k, 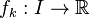 is an increasing function. If,
is an increasing function. If,
exists for all 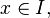 then,
then,
almost everywhere in I.[1]
In general, if we don't suppose fk is increasing for every k, in order to get the same conclusion, we need a stricter condition like uniform convergence of 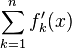 on I for every n.[2]
on I for every n.[2]
References
- 1 2 Jones, Frank (2001), Lebesgue Integration on Euclidean Space, Jones and Bartlett publishers, pp. 527–529.
- ↑ Rudin, Walter (1976), Principles of Mathematical Analysis, McGraw-Hill, p. 152.
This article is issued from Wikipedia - version of the 4/9/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.