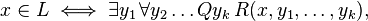Exponential hierarchy
In computational complexity theory, the exponential hierarchy is a hierarchy of complexity classes, which is an exponential time analogue of the polynomial hierarchy. As elsewhere in complexity theory, “exponential” is used in two different meanings (linear exponential bounds  for a constant c, and full exponential bounds
for a constant c, and full exponential bounds 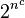 ), leading to two versions of the exponential hierarchy:[1][2]
), leading to two versions of the exponential hierarchy:[1][2]
- EH is the union of the classes
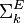 for all k, where
for all k, where 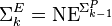 (i.e., languages computable in nondeterministic time
(i.e., languages computable in nondeterministic time  for some constant c with a
for some constant c with a 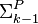 oracle). One also defines
oracle). One also defines 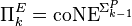 ,
, 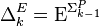 . An equivalent definition is that a language L is in
. An equivalent definition is that a language L is in 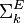 if and only if it can be written in the form
if and only if it can be written in the form
- where
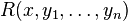 is a predicate computable in time
is a predicate computable in time  (which implicitly bounds the length of yi). Also equivalently, EH is the class of languages computable on an alternating Turing machine in time
(which implicitly bounds the length of yi). Also equivalently, EH is the class of languages computable on an alternating Turing machine in time  for some c with constantly many alternations.
for some c with constantly many alternations.
- EXPH is the union of the classes
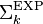 , where
, where 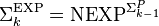 (languages computable in nondeterministic time
(languages computable in nondeterministic time 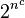 for some constant c with a
for some constant c with a 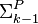 oracle), and again
oracle), and again 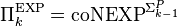 ,
, 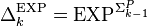 . A language L is in
. A language L is in 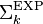 if and only if it can be written as
if and only if it can be written as
- where
 is computable in time
is computable in time 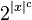 for some c, which again implicitly bounds the length of yi. Equivalently, EXPH is the class of languages computable in time
for some c, which again implicitly bounds the length of yi. Equivalently, EXPH is the class of languages computable in time 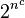 on an alternating Turing machine with constantly many alternations.
on an alternating Turing machine with constantly many alternations.
We have E ⊆ NE ⊆ EH ⊆ ESPACE, EXP ⊆ NEXP ⊆ EXPH ⊆ EXPSPACE, and EH ⊆ EXPH.
References
- ↑ Sarah Mocas, Separating classes in the exponential-time hierarchy from classes in PH, Theoretical Computer Science 158 (1996), no. 1–2, pp. 221–231.
- ↑ Anuj Dawar, Georg Gottlob, Lauri Hella, Capturing relativized complexity classes without order, Mathematical Logic Quarterly 44 (1998), no. 1, pp. 109–122.
External links
| ||||||||||||||||||||||
This article is issued from Wikipedia - version of the 2/15/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.