Dynamical theory of diffraction

The dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems. In a wider sense, similar treatment is related to the interaction of light with optical band-gap materials or related wave problems in acoustics.

Laue and Bragg geometries, top and bottom, as distinguished by the Dynamical theory of diffraction with the Bragg diffracted beam leaving the back or front surface of the crystal, respectively. (Ref.)

Reflectivities for Laue and Bragg geometries, top and bottom, respectively, as evaluated by the dynamical theory of diffraction for the absorption-less case. The flat top of the peak in Bragg geometry is the so-called Darwin Plateau. (Ref.)

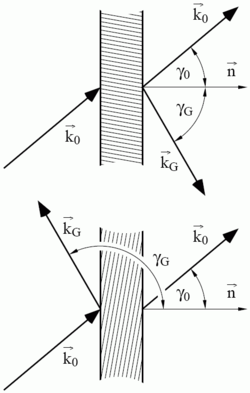
Principle of theory

The dynamical theory of diffraction considers the wave field in the periodic potential of the crystal and takes into account all multiple scattering effects. Unlike the kinematic theory of diffraction which describes the approximate position of Bragg or Laue diffraction peaks in reciprocal space, dynamical theory corrects for refraction, shape and width of the peaks, extinction and interference effects. Graphical representations are described in dispersion surfaces around reciprocal lattice points which fulfill the boundary conditions at the crystal interface.

Outcomes

• The crystal potential by itself leads to refraction and specular reflection of the waves at the interface to the crystal and delivers the refractive index off the Bragg reflection. It also corrects for refraction at the Bragg condition and combined Bragg and specular reflection in grazing incidence geometries.
• A Bragg reflection is the splitting of the dispersion surface at the border of the Brillouin zone in reciprocal space. There is a gap between the dispersion surfaces in which no travelling waves are allowed. For a non-absorbing crystal, the reflection curve shows a range of total reflection, the so-called Darwin plateau. Regarding the quantum mechanical energy of the system, this leads to the band gap structure which is commonly well known for electrons.
• Upon Laue diffraction, intensity is shuffled from the forward diffracted beam into the Bragg diffracted beam until extinction. The diffracted beam itself fulfills the Bragg condition and shuffles intensity back into the primary direction. This round-trip period is called the Pendellösung period.
• The extinction length is related to the Pendellösung period. Even if a crystal is infinitely thick, only the crystal volume within the extinction length contributes considerably to the diffraction in Bragg geometry.
• In Laue geometry, beam paths lie within the Borrmann triangle. Kato fringes are the intensity patterns due to Pendellösung effects at the exit surface of the crystal.
• Anomalous absorption effects take place due to a standing wave patterns of two wave fields. Absorption is stronger if the standing wave has its anti-nodes on the lattice planes, i.e. where the absorbing atoms are, and weaker, if the anti-nodes are shifted between the planes. The standing wave shifts from one condition to the other on each side of the Darwin plateau which gives the latter an asymmetric shape.

Applications

• X-ray diffraction
• Neutron diffraction
• Electron diffraction and transmission electron microscopy
• Structure determination in crystallography
• grazing incidence diffraction
• X-ray standing waves
• neutron and X-ray interferometry.
• synchrotron crystal optics
• neutron and X-ray diffraction topography
• X-ray imaging
• Crystal monochromators
• Electronic band structures

See also

• Volume hologram

Further reading

• J. Als-Nielsen, D. McMorrow: Elements of Modern X-ray physics. Wiley, 2001 (chapter 5: diffraction by perfect crystals).
• André Authier: Dynamical theory of X-ray diffraction. IUCr monographs on crystallography, no. 11. Oxford University Press (1st edition 2001/ 2nd edition 2003). ISBN 0-19-852892-2.
• R. W. James: The Optical Principles of the Diffraction of X-rays. Bell., 1948.
• M. von Laue: Röntgenstrahlinterferenzen. Akademische Verlagsanstalt, 1960 (German).
• Z. G. Pinsker: Dynamical Scattering of X-Rays in Crystals. Springer, 1978.
• B. E. Warren: X-ray diffraction. Addison-Wesley, 1969 (chapter 14: perfect crystal theory).
• W. H. Zachariasen: Theory of X-ray Diffraction in Crystals. Wiley, 1945.
• Boris W. Batterman, Henderson Cole: Dynamical Diffraction of X Rays by Perfect Crystals. Reviews of Modern Physics, Vol. 36, No. 3, 681-717, July 1964.
• H. Rauch, D. Petrascheck, “Grundlagen für ein Laue-Neutroneninterferometer Teil 1: Dynamische Beugung”, AIAU 74405b, Atominstitut der Österreichischen Universitäten, (1976)
• H. Rauch, D. Petrascheck, “Dynamical neutron diffraction and its application” in “Neutron Diffraction”, H. Dachs, Editor. (1978), Springer-Verlag: Berlin Heidelberg New York. p. 303.
• K.-D. Liss: "Strukturelle Charakterisierung und Optimierung der Beugungseigenschaften von Si(1-x)Ge(x) Gradientenkristallen, die aus der Gasphase gezogen wurden", Dissertation, Rheinisch Westfälische Technische Hochschule Aachen, (27 October 1994), urn:nbn:de:hbz:82-opus-2227