Dodd-Bullough-Mikhailov equation

Dodd-Bullough-Mikhailov equation is a nonlinear partial differential equation introduced by Roger Dodd, Robin Bullough, and Alexander Mikhailov.[1]

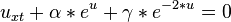
u_{xt}+\alpha*e^u+\gamma*e^{-2*u} = 0

In 2005 Mathematician Wazwar combined the Tzitzeica equation with Dodd-Bullough-Mikhailov equation into Tzitz´eica-Dodd-Bullough-Mikhailov equation.[2]

Dodd-Bullough-Mikhailov equation has traveling wave solutions.


References

  1. ↑ 李志斌编著 《非线性数学物理方程的行波解》 第105-107页，科学出版社 2008(Chinese)
  2. ↑ A.-M. Wazwaz, “The tanh method: solitons and periodic solutions for the Dodd-Bullough-Mikhailov and the Tzitz´eica- Dodd-Bullough equations,” Chaos, Solitons and Fractals, vol. 25,no. 1, pp. 55–63, 2005.
  1. Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
  2. Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
  3. Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
  4. Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
  5. Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
  6. Dongming Wang, Elimination Practice,Imperial College Press 2004
  7. David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
  8. George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759
This article is issued from Wikipedia - version of the 11/27/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.