Divergence of the sum of the reciprocals of the primes

The sum of the reciprocal of the primes increasing without bound. The x axis is in log scale, showing that the divergence is very slow. The red function is a lower bound that also diverges.

The sum of the reciprocals of all prime numbers diverges; that is:

\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty

This was proved by Leonhard Euler in 1737,^[1] and strengthens Euclid's 3rd-century-BC result that there are infinitely many prime numbers.

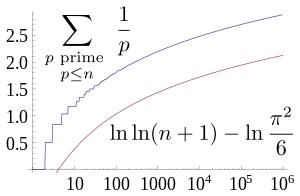
There are a variety of proofs of Euler's result, including a lower bound for the partial sums stating that

\sum _{\scriptstyle p{\text{ prime }} \atop \scriptstyle p\leq n}{\frac {1}{p}}\geq \log \log(n+1)-\log {\frac {\pi ^{2}}{6}}

for all natural numbers n. The double natural logarithm indicates that the divergence might be very slow, which is indeed the case. See Meissel–Mertens constant.

The harmonic series

First, we describe how Euler originally discovered the result. He was considering the harmonic series

\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots

He had already used the following "product formula" to show the existence of infinitely many primes.

\sum _{n=1}^{\infty }{\frac {1}{n}}=\prod _{p}{\frac {1}{1-p^{-1}}}=\prod _{p}\left(1+{\frac {1}{p}}+{\frac {1}{p^{2}}}+\cdots \right)

(Here, the product is taken over all primes p; in the following, a sum or product taken over p always represents a sum or product taken over a specified set of primes, unless noted otherwise.)

Such infinite products are today called Euler products. The product above is a reflection of the fundamental theorem of arithmetic. Of course, the above "equation" is not necessary because the harmonic series is known (by other means) to diverge.

Euler noted that if there were only a finite number of primes, then the product on the right would clearly converge, contradicting the divergence of the harmonic series. (In modern language, we now say that the existence of infinitely many primes is reflected by the fact that the Riemann zeta function has a simple pole at s = 1.)

Proofs

First

Euler takes the above product formula and proceeds to make a sequence of audacious leaps of logic. First, he takes the natural logarithm of each side, then he uses the Taylor series expansion for ln(x) as well as the sum of a converging series:

{\begin{aligned}\ln \left(\sum _{n=1}^{\infty }{\frac {1}{n}}\right)&{}=\ln \left(\prod _{p}{\frac {1}{1-p^{-1}}}\right)=-\sum _{p}\ln \left(1-{\frac {1}{p}}\right)\\&{}=\sum _{p}\left({\frac {1}{p}}+{\frac {1}{2p^{2}}}+{\frac {1}{3p^{3}}}+\cdots \right)\\&{}=\sum _{p}{\frac {1}{p}}+{\frac {1}{2}}\sum _{p}{\frac {1}{p^{2}}}+{\frac {1}{3}}\sum _{p}{\frac {1}{p^{3}}}+{\frac {1}{4}}\sum _{p}{\frac {1}{p^{4}}}+\cdots \\&{}=A+{\frac {1}{2}}B+{\frac {1}{3}}C+{\frac {1}{4}}D+\cdots \\&{}=A+K\end{aligned}}

for a fixed constant K < 1. Then he invokes the relation

\sum _{n=1}^{\infty }{\frac {1}{n}}=\ln \infty ,

which he explains, for instance in a later 1748 work,^[2] by setting x=1 in the Taylor series expansion

\ln \left({\frac {1}{1-x}}\right)=\sum _{n=1}^{\infty }{\frac {x^{n}}{n}}.

This allows him to conclude

A={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+\cdots =\ln \ln \infty .

It is almost certain that Euler meant that the sum of the reciprocals of the primes less than n is asymptotic to ln(ln(n)) as n approaches infinity. It turns out this is indeed the case, and a more precise version of this fact was rigorously proved by Franz Mertens in 1874.^[3] Thus Euler obtained a correct result by questionable means.

Second

The following proof by contradiction is due to Paul Erdős.

Let p_i denote the i^th prime number. Assume that the sum of the reciprocals of the primes converges; i.e.,

\sum _{i=1}^{\infty }{1 \over p_{i}}<\infty

Then there exists a smallest positive integer k such that

\sum _{i=k+1}^{\infty }{1 \over p_{i}}<{1 \over 2}\qquad (1)

For a positive integer x let M_x denote the set of those n in {1, 2, . . ., x} which are not divisible by any prime greater than p_k (or equivalently all n ≤ x which are a product of powers of primes p_i ≤ p_k). We will now derive an upper and a lower estimate for |M_x|, the number of elements in M_x. For large x, these bounds will turn out to be contradictory.

Upper estimate

Every n in M_x can be written as n = r m² with positive integers m and r, where r is square-free. Since only the k primes p₁, …, p_k can show up (with exponent 1) in the prime factorization of r, there are at most 2^k different possibilities for r. Furthermore, there are at most √x possible values for m. This gives us the upper estimate

|M_{x}|\leq 2^{k}{\sqrt {x}}\qquad (2)

Lower estimate

The remaining x − |M_x| numbers in the set difference {1, 2, . . ., x} \ M_x are all divisible by a prime greater than p_k. Let N_i,x denote the set of those n in {1, 2, . . ., x} which are divisible by the i^th prime p_i. Then

\{1,2,\ldots ,x\}\setminus M_{x}=\bigcup _{i=k+1}^{\infty }N_{i,x}

Since the number of integers in N_i,x is at most x/p_i (actually zero for p_i > x), we get

x-|M_{x}|\leq \sum _{i=k+1}^{\infty }|N_{i,x}|<\sum _{i=k+1}^{\infty }{x \over p_{i}}

Using (1), this implies

{x \over 2}<|M_{x}|\qquad (3)

Contradiction

When x ≥ 2^2k + 2, the estimates (2) and (3) cannot both hold, because ${\tfrac {x}{2}}\geq 2^{k}{\sqrt {x}}$ .

Third

Here is another proof that actually gives a lower estimate for the partial sums; in particular, it shows that these sums grow at least as fast as log(log(n)). The proof is an adaptation of the product expansion idea of Euler. In the following, a sum or product taken over p always represents a sum or product taken over a specified set of primes.

The proof rests upon the following four inequalities:

Every positive integer i can be uniquely expressed as the product of a square-free integer and a square. This gives the inequality

\sum _{i=1}^{n}{\frac {1}{i}}\leq \prod _{p\leq n}{\left(1+{\frac {1}{p}}\right)}\sum _{k=1}^{n}{\frac {1}{k^{2}}}

where for every i between 1 and n the (expanded) product corresponds to the square-free part of i and the sum corresponds to the square part of i (see fundamental theorem of arithmetic).

The upper estimate for the natural logarithm

\log(n+1)=\int _{1}^{n+1}{\frac {dx}{x}}=\sum _{i=1}^{n}\underbrace {\int _{i}^{i+1}{\frac {dx}{x}}} _{{}\,<\,1/i}<\sum _{i=1}^{n}{\frac {1}{i}}

The lower estimate 1 + x < exp(x) for the exponential function, which holds for all x > 0.
Let n ≥ 2. The upper bound (using a telescoping sum) for the partial sums (convergence is all we really need)

\sum _{k=1}^{n}{\frac {1}{k^{2}}}<1+\sum _{k=2}^{n}\underbrace {\left({\frac {1}{k-{\frac {1}{2}}}}-{\frac {1}{k+{\frac {1}{2}}}}\right)} _{=\,1/(k^{2}-1/4)\,>\,1/k^{2}}=1+{\frac {2}{3}}-{\frac {1}{n+{\frac {1}{2}}}}<{\frac {5}{3}}

Combining all these inequalities, we see that

{\begin{aligned}\log(n+1)&<\sum _{i=1}^{n}{\frac {1}{i}}\\&\leq \prod _{p\leq n}{\left(1+{\frac {1}{p}}\right)}\sum _{k=1}^{n}{\frac {1}{k^{2}}}\\&<{\frac {5}{3}}\prod _{p\leq n}{\exp \left({\frac {1}{p}}\right)}\\&={\frac {5}{3}}\exp \left(\sum _{p\leq n}{\frac {1}{p}}\right)\end{aligned}}

Dividing through by 5/3 and taking the natural logarithm of both sides gives

\log \log(n+1)-\log {\frac {5}{3}}<\sum _{p\leq n}{\frac {1}{p}}

as desired. ∎

Using

\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}={\frac {\pi ^{2}}{6}}

(see Basel problem), the above constant ln (5/3) = 0.51082… can be improved to ln(π²/6) = 0.4977…; in fact it turns out that

\lim _{n\to \infty }\left(\sum _{p\leq n}{\frac {1}{p}}-\log \log(n)\right)=M

where M = 0.261497… is the Meissel–Mertens constant (somewhat analogous to the much more famous Euler–Mascheroni constant).

Fourth

From Dusart's inequality, we get

p_{n}<n\log n+n\log \log n\quad {\mbox{for }}n\geq 6

Then

{\begin{aligned}\sum _{n=1}^{\infty }{\frac {1}{p_{n}}}&\geq \sum _{n=6}^{\infty }{\frac {1}{p_{n}}}\\&\geq \sum _{n=6}^{\infty }{\frac {1}{n\log n+n\log \log n}}\\&\geq \sum _{n=6}^{\infty }{\frac {1}{2n\log n}}\\&=\infty \end{aligned}}

by the integral test for convergence. This shows that the series on the left diverges.

Partial sums

While the partial sums of the reciprocals of the primes eventually exceed any integer value, they never equal an integer.

One proof^[4] is by induction: The first partial sum is ${\frac {1}{2}},$ which has the form ${\frac {\text{odd}}{\text{even}}}={\frac {O_{1}}{E_{1}}}$ where O and E refer to odd and even numbers respectively. If the n^th partial sum has the form ${\frac {O_{n}}{E_{n}}},$ then the (n+1)^st one equals ${\frac {O_{n}}{E_{n}}}+{\frac {1}{p_{n+1}}}={\frac {O_{n}p_{n+1}+E_{n}}{E_{n}p_{n+1}}}={\frac {O_{n+1}}{E_{n+1}}}$ for the (n+1)^st prime $p_{{n+1}};$ since this repeats the odd-over-even form, this partial sum cannot be an integer (because 2 divides the denominator but not the numerator), and the induction continues.

Another proof rewrites the expression for the sum of the first n reciprocals of primes (or indeed the sum of the reciprocals of any set of primes) in terms of the least common denominator, which is the product of all these primes. Then each of these primes divides all but one of the numerator terms and hence does not divide the numerator itself; but each prime does divide the denominator. Thus the expression is irreducible and is non-integer.

References

↑ Leonhard Euler. "Variae observationes circa series infinitas". Commentarii Academiae Scientarum Petropolitanae 9 (1737), 160-188.
↑ Leonhard Euler. "Introductio in Analysin Infinitorum. Tomus Primus". Bousquet, Lausanne 1748. Exemplum 1, p. 228.
↑ Mertens, F. (1874). "Ein Beitrag zur analytischer Zahlentheorie". J. Reine. Angew. Math. 78: 46–62.
↑ Lord, Nick (2015). "Quick proofs that certain sums of fractions are not integers". The Mathematical Gazette. 99: 128–130. doi:10.1017/mag.2014.16.

Sources

William Dunham (1999). Euler The Master of Us All. MAA. pp. 61–79. ISBN 0-88385-328-0.

External links

Chris K. Caldwell: There are infinitely many primes, but, how big of an infinity?

Sequences and series

Integer
sequences

Basic	Arithmetic progression Geometric progression Square number Cubic number Factorial Powers of two Powers of 10

Advanced	Complete sequence Fibonacci numbers Figurate number Heptagonal number Hexagonal number Lucas number Pell number Pentagonal number Polygonal number Triangular number others

Properties of sequences

Properties of series

Explicit series

Convergent	1/2 − 1/4 + 1/8 − 1/16 + ⋯ 1/2 + 1/4 + 1/8 + 1/16 + ⋯ 1/4 + 1/16 + 1/64 + 1/256 + ⋯ 1 + 1/1^s + 1/2^s+ 1/3^s + ... (Riemann zeta function)

Divergent	1 + 1 + 1 + 1 + ⋯ 1 + 2 + 3 + 4 + ⋯ 1 + 2 + 4 + 8 + ⋯ 1 − 1 + 1 − 1 + ⋯ (Grandi's series) Infinite arithmetic series 1 − 2 + 3 − 4 + ⋯ 1 − 2 + 4 − 8 + ⋯ 1 + 1/2 + 1/3 + 1/4 + ⋯ (harmonic series) 1 − 1 + 2 − 6 + 24 − 120 + ⋯ (alternating factorials) 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ⋯ (inverses of primes)

Kinds of series

Hypergeometric
series

This article is issued from Wikipedia - version of the 6/28/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.