Community structure
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
|
||||
In the study of complex networks, a network is said to have community structure if the nodes of the network can be easily grouped into (potentially overlapping) sets of nodes such that each set of nodes is densely connected internally. In the particular case of non-overlapping community finding, this implies that the network divides naturally into groups of nodes with dense connections internally and sparser connections between groups. But overlapping communities are also allowed. The more general definition is based on the principle that pairs of nodes are more likely to be connected if they are both members of the same community(ies), and less likely to be connected if they do not share communities. A related but different problem is community search, here the goal is to find a community that a certain vertex belongs to.
Properties
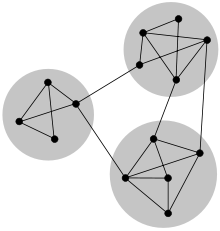
In the study of networks, such as computer and information networks, social networks and biological networks, a number of different characteristics have been found to occur commonly, including the small-world property, heavy-tailed degree distributions, and clustering, among others. Another common characteristic is community structure.[1][2][3][4] In the context of networks, community structure refers to the occurrence of groups of nodes in a network that are more densely connected internally than with the rest of the network, as shown in the example image to the right. This inhomogeneity of connections suggests that the network has certain natural divisions within it.
Communities are often defined in terms of the partition of the set of vertices, that is each node is put into one and only one community, just as in the figure. This is a useful simplification and most community detection methods find this type of community structure. However, in some cases a better representation could be one where vertices are in more than one community. This might happen in a social network where each vertex represents a person, and the communities represent the different groups of friends: one community for family, another community for co-workers, one for friends in the same sports club, and so on. The use of cliques for community detection discussed below is just one example of how such overlapping community structure can be found.
Some networks may not have any meaningful community structure. Many basic network models, for example, such as the random graph and the Barabási–Albert model, do not display community structure.
Applications
Community structures are quite common in real networks. Social networks include community groups (the origin of the term, in fact) based on common location, interests, occupation, etc.[5] Metabolic networks have communities based on functional groupings. Citation networks form communities by research topic.[1] Being able to identify these sub-structures within a network can provide insight into how network function and topology affect each other. Such insight can be useful in improving some algorithms on graphs such as spectral clustering.[6]
Algorithms for finding communities
Finding communities within an arbitrary network can be a computationally difficult task. The number of communities, if any, within the network is typically unknown and the communities are often of unequal size and/or density. Despite these difficulties, however, several methods for community finding have been developed and employed with varying levels of success.[4]
Minimum-cut method
One of the oldest algorithms for dividing networks into parts is the minimum cut method (and variants such as ratio cut and normalized cut). This method sees use, for example, in load balancing for parallel computing in order to minimize communication between processor nodes.
In the minimum-cut method, the network is divided into a predetermined number of parts, usually of approximately the same size, chosen such that the number of edges between groups is minimized. The method works well in many of the applications for which it was originally intended but is less than ideal for finding community structure in general networks since it will find communities regardless of whether they are implicit in the structure, and it will find only a fixed number of them.[7]
Hierarchical clustering
Another method for finding community structures in networks is hierarchical clustering. In this method one defines a similarity measure quantifying some (usually topological) type of similarity between node pairs. Commonly used measures include the cosine similarity, the Jaccard index, and the Hamming distance between rows of the adjacency matrix. Then one groups similar nodes into communities according to this measure. There are several common schemes for performing the grouping, the two simplest being single-linkage clustering, in which two groups are considered separate communities if and only if all pairs of nodes in different groups have similarity lower than a given threshold, and complete linkage clustering, in which all nodes within every group have similarity greater than a threshold. A novel approach in this direction is the use of various similarity or dissimilarity measures, combined through convex sums,[8] which has greatly improved the performance of this kind of methodology.
Girvan–Newman algorithm
Another commonly used algorithm for finding communities is the Girvan–Newman algorithm.[1] This algorithm identifies edges in a network that lie between communities and then removes them, leaving behind just the communities themselves. The identification is performed by employing the graph-theoretic measure betweenness centrality, which assigns a number to each edge which is large if the edge lies "between" many pairs of nodes.
The Girvan–Newman algorithm returns results of reasonable quality and is popular because it has been implemented in a number of standard software packages. But it also runs slowly, taking time O(m2n) on a network of n vertices and m edges, making it impractical for networks of more than a few thousand nodes.[9]
Modularity maximization
In spite of its known drawbacks, one of the most widely used methods for community detection is modularity maximization.[9] Modularity is a benefit function that measures the quality of a particular division of a network into communities. The modularity maximization method detects communities by searching over possible divisions of a network for one or more that have particularly high modularity. Since exhaustive search over all possible divisions is usually intractable, practical algorithms are based on approximate optimization methods such as greedy algorithms, simulated annealing, or spectral optimization, with different approaches offering different balances between speed and accuracy.[10][11] A popular modularity maximization approach is the Louvain method, which iteratively optimizes local communities until global modularity can no longer be improved given perturbations to the current community state.[12] The currently best modularity maximization algorithm (winner of the 10th DIMACS Implementation Challenge) is an iterative ensemble algorithm.[13]
The usefulness of modularity optimization is questionable, as it has been shown that modularity optimization often fails to detect clusters smaller than some scale, depending on the size of the network (resolution limit[14]); on the other hand the landscape of modularity values is characterized by a huge degeneracy of partitions with high modularity, close to the absolute maximum, which may be very different from each other.[15]
Statistical inference
Methods based on statistical inference attempt to fit a generative model to the network data, which encodes the community structure. The overall advantage of this approach compared to the alternatives is its more principled nature, and the capacity to inherently address issues of statistical significance. Most methods in the literature are based on the stochastic block model[16] as well as variants including mixed membership,[17][18] degree-correction,[19] and hierarchical structures.[20] Model selection can be performed using principled approaches such as minimum description length[21][22] and Bayesian model selection.[23] Currently many algorithms exist to perform efficient inference of stochastic block models, including belief propagation[24][25] and agglomerative Monte Carlo.[26]
Differently from approaches which attempt to cluster the network given an ad-hoc quality function, this class of methods is based on generative models which not only serve as a description of the large-scale structure of the network, but also can be used to generalize the data, and predict the occurrence of missing or spurious links in the network.[27][28]
Clique-based methods
Cliques are subgraphs in which every node is connected to every other node in the clique. As nodes can not be more tightly connected than this, it is not surprising that there are many approaches to community detection in networks based on the detection of cliques in a graph and the analysis of how these overlap. Note that as a node can be a member of more than one clique, a node can be a member of more than one community in these methods giving an overlapping community structure.
One approach is to find the maximal cliques, that is find the cliques which are not the subgraph of any other clique. The classic algorithm to find these is the Bron–Kerbosch algorithm. The overlap of these can be used to define communities in several ways. The simplest is to consider only maximal cliques bigger than a minimum size (number of nodes). The union of these cliques then defines a subgraph whose components (disconnected parts) then define communities.[29] Such approaches are often implemented in social network analysis software such as UCInet.
The alternative approach to is to use cliques of fixed size, k. The overlap of these can be used to define a type of k-regular hypergraph or a structure which is a generalisation of the line graph (the case when k=2) known as a Clique graph.[30] The clique graphs have vertices which represent the cliques in the original graph while the edges of the clique graph record the overlap of the clique in the original graph. Applying any of the previous community detection methods (which assign each node to a community) to the clique graph then assigns each clique to a community. This can then be used to determine community membership of nodes in the cliques. Again as a node may be in several cliques, it can be a member of several communities. For instance the clique percolation method[31] defines communities as percolation clusters of k-cliques. To do this it finds all k-cliques in a network, that is all the complete sub-graphs of k-nodes. It then defines two k-cliques to be adjacent if they share k − 1 nodes, that is this is used to define edges in a clique graph. A community is then defined to be the maximal union of k-cliques in which we can reach any k-clique from any other k-clique through series of k-clique adjacencies. That is communities are just the connected components in the clique graph. Since a node can belong to several different k-clique percolation clusters at the same time, the communities can overlap with each other.
Testing methods of finding communities algorithms
The evaluation of algorithms, to detect which are better at detecting community structure, is still an open question. It must be based on analyses of networks of known structure. A typical example is the "four groups" test, in which a network is divided into four equally-sized groups (usually of 32 nodes each) and the probabilities of connection within and between groups varied to create more or less challenging structures for the detection algorithm. Such benchmark graphs are a special case of the planted l-partition model[32] of Condon and Karp, or more generally of "stochastic block models," a general class of random network models containing community structure. Other more flexible benchmarks have been proposed that allow for varying group sizes and nontrivial degree distributions, such as LFR benchmark proposed by Lancichinetti et al. ,[33] which is an extension of the four groups benchmark that includes heterogeneous distributions of node degree and community size, making it a more severe test of community detection methods.
Commonly used computer-generated benchmarks start with a network of well-defined communities. Then, this structure is degraded by rewiring or removing links and it gets harder and harder for the algorithms to detect the original partition. At the end, the network reaches a point where it is essentially random. This kind of benchmark may be called "open". The performance on these benchmarks is evaluated by measures such as normalized mutual information or variation of information. They compare the solution obtained by an algorithm with the original community structure, evaluating the similarity of both partitions.
See also
References
- 1 2 3 M. Girvan; M. E. J. Newman (2002). "Community structure in social and biological networks". Proc. Natl. Acad. Sci. USA. 99 (12): 7821–7826. doi:10.1073/pnas.122653799. PMC 122977
 . PMID 12060727.
. PMID 12060727. - ↑ S. Fortunato (2010). "Community detection in graphs". Phys. Rep. 486 (3-5): 75–174. doi:10.1016/j.physrep.2009.11.002.
- ↑ F. D. Malliaros; M. Vazirgiannis (2013). "Clustering and community detection in directed networks: A survey". Phys. Rep. 533 (4): 95–142. doi:10.1016/j.physrep.2013.08.002.
- 1 2 M. A. Porter; J.-P. Onnela; P. J. Mucha (2009). "Communities in Networks" (PDF). Not. Amer. Math. Soc. 56: 1082–1097, 1164–1166.
- ↑ Hamdaqa, Mohammad; Tahvildari, Ladan; LaChapelle, Neil; Campbell, Brian (2014). "Cultural Scene Detection Using Reverse Louvain Optimization". Science of Computer Programming. 95: 44–72. doi:10.1016/j.scico.2014.01.006.
- ↑ Zare, Habil; P. Shooshtari; A. Gupta; R. Brinkman (2010). "Data reduction for spectral clustering to analyze high throughput flow cytometry data". BMC Bioinformatics. 11 (1): 403. doi:10.1186/1471-2105-11-403. PMC 2923634
 . PMID 20667133.
. PMID 20667133. - ↑ M. E. J. Newman (2004). "Detecting community structure in networks". Eur. Phys. J. B. 38 (2): 321–330. doi:10.1140/epjb/e2004-00124-y.
- ↑ Alvarez, Alejandro J.; Sanz-Rodríguez, Carlos E.; Cabrera, Juan Luis (2015-12-13). "Weighting dissimilarities to detect communities in networks". Phil. Trans. R. Soc. A. 373 (2056): 20150108. doi:10.1098/rsta.2015.0108. ISSN 1364-503X. PMID 26527808.
- 1 2 M. E. J. Newman (2004). "Fast algorithm for detecting community structure in networks". Phys. Rev. E. 69 (6): 066133. doi:10.1103/PhysRevE.69.066133.
- ↑ L. Danon; J. Duch; A. Díaz-Guilera; A. Arenas (2005). "Comparing community structure identification". J. Stat. Mech. 2005 (09): P09008. doi:10.1088/1742-5468/2005/09/P09008.
- ↑ R. Guimera; L. A. N. Amaral (2004). "Functional cartography of complex metabolic networks". Nature. 433 (7028): 895–900. doi:10.1038/nature03288.
- ↑ V.D. Blondel; J.-L. Guillaume; R. Lambiotte; E. Lefebvre (2008). "Fast unfolding of community hierarchies in large networks". J. Stat. Mech. 2008 (10): P10008. doi:10.1088/1742-5468/2008/10/P10008.
- ↑ Michael Ovelgönne; Andreas Geyer-Schulz (2013). "An ensemble learning strategy for graph clustering". Graph Partitioning and Graph Clustering. Contemporary Mathematics. American Mathematical Society. 588: 187–206. doi:10.1090/conm/588.
- ↑ S. Fortunato; M. Barthelemy (2007). "Resolution limit in community detection". Proceedings of the National Academy of Sciences of the United States of America. 104 (1): 36–41. doi:10.1073/pnas.0605965104. PMC 1765466
 . PMID 17190818.
. PMID 17190818.
- ↑ B. H. Good; Y.-A. de Montjoye; A. Clauset (2010). "The performance of modularity maximization in practical contexts". Phys. Rev. E. 81 (4): 046106. doi:10.1103/PhysRevE.81.046106.
- ↑ Holland, Paul W.; Kathryn Blackmond Laskey; Samuel Leinhardt (June 1983). "Stochastic blockmodels: First steps". Social Networks. 5 (2): 109–137. doi:10.1016/0378-8733(83)90021-7. ISSN 0378-8733. Retrieved 2011-08-26.
- ↑ Airoldi, Edoardo M.; David M. Blei; Stephen E. Fienberg; Eric P. Xing (June 2008). "Mixed Membership Stochastic Blockmodels". J. Mach. Learn. Res. 9: 1981–2014. ISSN 1532-4435. Retrieved 2013-10-09.
- ↑ Ball, Brian; Brian Karrer; M. E. J. Newman (2011). "Efficient and principled method for detecting communities in networks". Physical Review E. 84 (3): 036103. doi:10.1103/PhysRevE.84.036103. Retrieved 2011-12-08.
- ↑ Karrer, Brian; M. E. J. Newman (2011-01-21). "Stochastic blockmodels and community structure in networks". Physical Review E. 83 (1): 016107. doi:10.1103/PhysRevE.83.016107. Retrieved 2011-11-08.
- ↑ Peixoto, Tiago P. (2014-03-24). "Hierarchical Block Structures and High-Resolution Model Selection in Large Networks". Physical Review X. 4 (1): 011047. doi:10.1103/PhysRevX.4.011047. Retrieved 2014-04-24.
- ↑ Martin Rosvall; Carl T. Bergstrom (2007). "An information-theoretic framework for resolving community structure in complex networks". Proceedings of the National Academy of Sciences of the United States of America. 104 (18): 7327–7331. doi:10.1073/pnas.0611034104.
- ↑ De Domenico, M.; Lancichinetti, A.; Arenas, A.; Rosvall, M. (6 March 2015). "Identifying Modular Flows on Multilayer Networks Reveals Highly Overlapping Organization in Interconnected Systems". Phys. Rev. X 5, 011027 (2015). doi:10.1103/PhysRevX.5.011027.
- ↑ Yan, Xiaoran; Jacob E. Jensen; Florent Krzakala; Cristopher Moore; Cosma Rohilla Shalizi; Lenka Zdeborova; Pan Zhang; Yaojia Zhu (2012-07-17). "Model Selection for Degree-corrected Block Models". arXiv:1207.3994
 .
. - ↑ Gopalan, Prem K.; David M. Blei (2013-09-03). "Efficient discovery of overlapping communities in massive networks". Proceedings of the National Academy of Sciences. 110 (36): 14534–14539. doi:10.1073/pnas.1221839110. ISSN 0027-8424. PMC 3767539
 . PMID 23950224. Retrieved 2013-10-09.
. PMID 23950224. Retrieved 2013-10-09. - ↑ Decelle, Aurelien; Florent Krzakala; Cristopher Moore; Lenka Zdeborová (2011-12-12). "Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications". Physical Review E. 84 (6): 066106. doi:10.1103/PhysRevE.84.066106. Retrieved 2012-01-16.
- ↑ Peixoto, Tiago P. (2014-01-13). "Efficient Monte Carlo and greedy heuristic for the inference of stochastic block models". Physical Review E. 89 (1): 012804. doi:10.1103/PhysRevE.89.012804. Retrieved 2014-01-21.
- ↑ Guimerà, Roger; Marta Sales-Pardo (2009-12-29). "Missing and spurious interactions and the reconstruction of complex networks". Proceedings of the National Academy of Sciences. 106 (52): 22073–22078. doi:10.1073/pnas.0908366106. Retrieved 2011-11-09.
- ↑ Clauset, Aaron; Cristopher Moore; M. E. J. Newman (2008-05-01). "Hierarchical structure and the prediction of missing links in networks". Nature. 453 (7191): 98–101. doi:10.1038/nature06830. ISSN 0028-0836.
- ↑ M.G. Everett; S.P. Borgatti (1998). "Analyzing Clique Overlap Connections". Connections. 21: 49.
- ↑ T.S. Evans (2010). "Clique Graphs and Overlapping Communities". J. Stat. Mech. 2010 (12): P12037. arXiv:1009.0638
 . doi:10.1088/1742-5468/2010/12/P12037.
. doi:10.1088/1742-5468/2010/12/P12037.
- ↑ G. Palla; I. Derényi; I. Farkas; T. Vicsek (2005). "Uncovering the overlapping community structure of complex networks in nature and society". Nature. 435 (7043): 814–818. doi:10.1038/nature03607. PMID 15944704.
- ↑ Condon, A.; Karp, R. M. (2001). "Algorithms for graph partitioning on the planted partition model". Random Struct. Algor. 18 (2): 116–140. doi:10.1002/1098-2418(200103)18:2<116::AID-RSA1001>3.0.CO;2-2.
- ↑ A. Lancichinetti; S. Fortunato; F. Radicchi (2008). "Benchmark graphs for testing community detection algorithms". Phys. Rev. E. 78 (4): 046110. doi:10.1103/PhysRevE.78.046110.
External links
- Community detection in graphs – an introduction
- Are there implementations of algorithms for community detection in graphs? – Stack Overflow
- What are the differences between community detection algorithms in igraph? – Stack Overflow
