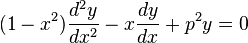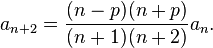Chebyshev equation

Chebyshev's equation is the second order linear differential equation

(1-x^2) {d^2 y \over d x^2} - x {d y \over d x} + p^2 y = 0

where p is a real constant. The equation is named after Russian mathematician Pafnuty Chebyshev.

The solutions are obtained by power series:

y = \sum_{n=0}^\infty a_nx^n

where the coefficients obey the recurrence relation

a_{n+2} = {(n-p) (n+p) \over (n+1) (n+2) } a_n.

These series converge for x in $[-1, 1]$ , as may be seen by applying the ratio test to the recurrence.

The recurrence may be started with arbitrary values of a₀ and a₁, leading to the two-dimensional space of solutions that arises from second order differential equations. The standard choices are:

a₀ = 1 ; a₁ = 0, leading to the solution

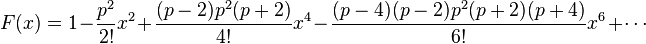
F(x) = 1 - \frac{p^2}{2!}x^2 + \frac{(p-2)p^2(p+2)}{4!}x^4 - \frac{(p-4)(p-2)p^2(p+2)(p+4)}{6!}x^6 + \cdots

and

a₀ = 0 ; a₁ = 1, leading to the solution

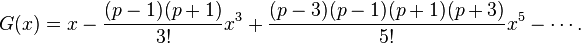
G(x) = x - \frac{(p-1)(p+1)}{3!}x^3 + \frac{(p-3)(p-1)(p+1)(p+3)}{5!}x^5 - \cdots.

The general solution is any linear combination of these two.

When p is an integer, one or the other of the two functions has its series terminate after a finite number of terms: F terminates if p is even, and G terminates if p is odd. In this case, that function is a p^th degree polynomial (converging everywhere, of course), and that polynomial is proportional to the p^th Chebyshev polynomial.

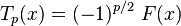T_p(x) = (-1)^{p/2}\ F(x)\,

if p is even

T_p(x) = (-1)^{(p-1)/2}\ p\ G(x)\,

if p is odd

This article incorporates material from Chebyshev equation on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the 4/23/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.