Blum–Micali algorithm

The Blum–Micali algorithm is a cryptographically secure pseudorandom number generator. The algorithm gets its security from the difficulty of computing discrete logarithms.^[1]

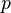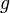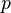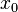Let $p$ be an odd prime, and let $g$ be a primitive root modulo $p$ . Let $x_0$ be a seed, and let

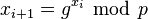$x_{i+1} = g^{x_i}\ \bmod{\ p}$ .

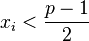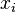The $i$ th output of the algorithm is 1 if $x_i < \frac{p-1}{2}$ . Otherwise the output is 0. This is equivalent to using one bit of $x_i$ as your random number. It has been shown that 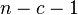$n - c - 1$ bits of 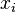$x_i$ can be used if solving the discrete log problem is infeasible even for exponents with as few as $c$ bits.^[2]

In order for this generator to be secure, the prime number 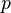$p$ needs to be large enough so that computing discrete logarithms modulo 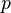$p$ is infeasible.^[1] To be more precise, any method that predicts the numbers generated will lead to an algorithm that solves the discrete logarithm problem for that prime.^[3]

There is a paper discussing possible examples of the quantum permanent compromise attack to the Blum-Micali construction. This attacks illustrate how a previous attack to the Blum-Micali generator can be extended to the whole Blum-Micali construction, including the Blum Blum Shub and Kaliski generators.^[4]

References

↑ 1.0 1.1 Bruce Schneier, Applied Cryptography: Protocols, Algorithms, and Source Code in C, pages 416-417, Wiley; 2nd edition (October 18, 1996), ISBN 0471117099
↑ An improved pseudo-random generator based on the discrete logarithm problem R Gennaro - Journal of Cryptology, 2005 - Springer
↑ Manuel Blum and Silvio Micali, How to Generate Cryptographically Strong Sequences of Pseudorandom Bits, SIAM Journal on Computing 13, no. 4 (1984): 850-864. online (pdf)
↑ Elloá B. Guedes, Francisco Marcos de Assis, Bernardo Lula Jr, Examples of the Generalized Quantum Permanent Compromise Attack to the Blum-Micali Construction http://arxiv.org/abs/1012.1776

External links

http://crypto.stanford.edu/pbc/notes/crypto/blummicali.xhtml

This article is issued from Wikipedia - version of the 5/22/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.