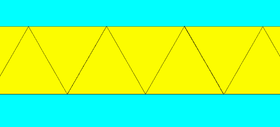
Apeirogonal prism

Apeirogonal prism
Type	Semiregular tiling
Vertex configuration	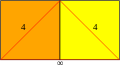4.4.∞
Schläfli symbol	t{2,∞}
Wythoff symbol	2 ∞ | 2
Coxeter diagram
Symmetry	[∞,2], (*∞22)
Rotation symmetry	[∞,2]+, (∞22)
Bowers acronym	Azip
Dual	Apeirogonal dipyramid
Properties	Vertex-transitive

In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane.^[1]

Thorold Gosset called it a 2-dimensional semi-check, like a single row of a checkerboard.

If the sides are squares, it is a uniform tiling. In general, it can have two sets of alternating congruent rectangles.

Its truncated form can have alternate colored square faces:

Its dual tiling is an apeirogonal bipyramid:

Related tilings and polyhedra

The apeirogonal tiling is the arithmetic limit of the family of prisms t{2, p} or p.4.4, as p tends to infinity, thereby turning the prism into a Euclidean tiling.

An alternation operation can create an apeirogonal antiprism composed of three triangles and one apeirogon at each vertex.

Similarly to the uniform polyhedra and the uniform tilings, eight uniform tilings may be based from the regular apeirogonal tiling. The rectified and cantellated forms are duplicated, and as two times infinity is also infinity, the truncated and omnitruncated forms are also duplicated, therefore reducing the number of unique forms to four: the apeirogonal tiling, the apeirogonal hosohedron, the apeirogonal prism, and the apeirogonal antiprism.

(∞ 2 2)	Parent	Truncated	Rectified	Bitruncated	Birectified (dual)	Cantellated	Omnitruncated (Cantitruncated)	Snub
Wythoff	2 | ∞ 2	2 2 | ∞	2 | ∞ 2	2 ∞ | 2	∞ | 2 2	∞ 2 | 2	∞ 2 2 |	| ∞ 2 2
Schläfli	t0{∞,2}	t0,1{∞,2}	t1{∞,2}	t1,2{∞,2}	t2{∞,2}	t0,2{∞,2}	t0,1,2{∞,2}	s{∞,2}
Coxeter
Image Vertex figure	{∞,2}	∞.∞	∞.∞	4.4.∞	{2,∞}	4.4.∞	4.4.∞	3.3.3.∞

Notes

References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. 
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5

Tessellation
Periodic Pythagorean Rhombille Schwarz triangle Rectangle Domino Uniform tiling & honeycomb Coloring Convex Kisrhombille Wallpaper group Wythoff
Aperiodic Ammann–Beenker Aperiodic set of prototiles List Einstein problem Socolar–Taylor Gilbert Penrose Pentagonal Pinwheel Quaquaversal Rep-tile & Self-tiling Sphinx Truchet
Other Anisohedral & Isohedral Architectonic & catoptric Circle Limit III Computer graphics Honeycomb Isotoxal Packing Problems Domino Wang Heesch's Squaring Prototile Conway criterion Girih Regular Division of the Plane Regular grid Substitution Voronoi Voderberg
By vertex type Spherical 2n 33.n V33.n 42.n V42.n Regular 2∞ 36 44 63 Semi- regular 32.4.3.4 V32.4.3.4 33.42 33.∞ 34.6 V34.6 3.4.6.4 (3.6)2 3.122 42.∞ 4.6.12 4.82 Hyper- bolic 32.4.3.5 32.4.3.6 32.4.3.7 32.4.3.8 32.4.3.∞ 32.5.3.5 32.5.3.6 32.6.3.6 32.6.3.8 32.7.3.7 32.8.3.8 33.4.3.4 32.∞.3.∞ 34.7 34.8 34.∞ 35.4 37 38 3∞ (3.4)3 (3.4)4 3.4.62.4 3.4.7.4 3.4.8.4 3.4.∞.4 3.6.4.6 (3.7)2 (3.8)2 3.142 3.162 (3.∞)2 3.∞2 42.5.4 42.6.4 42.7.4 42.8.4 42.∞.4 45 46 47 48 4∞ (4.5)2 (4.6)2 4.6.12 4.6.14 V4.6.14 4.6.16 V4.6.16 4.6.∞ (4.7)2 (4.8)2 4.8.10 V4.8.10 4.8.12 4.8.14 4.8.16 4.8.∞ 4.102 4.10.12 4.122 4.12.16 4.142 4.162 4.∞2 (4.∞)2 54 55 56 5∞ 5.4.6.4 (5.6)2 5.82 5.102 5.122 (5.∞)2 64 65 66 68 6.4.8.4 (6.8)2 6.82 6.102 6.122 6.162 73 74 77 7.62 7.82 7.142 83 84 86 88 812 8.62 8.162 ∞3 ∞4 ∞5 ∞∞ ∞.62 ∞.82