Almost simple group

In mathematics, a group is said to be almost simple if it contains a non-abelian simple group and is contained within the automorphism group of that simple group: if it fits between a (non-abelian) simple group and its automorphism group. In symbols, a group A is almost simple if there is a simple group S such that 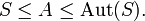$S \leq A \leq \operatorname{Aut}(S).$

Examples

Trivially, nonabelian simple groups and the full group of automorphisms are almost simple, but proper examples exist, meaning almost simple groups that are neither simple nor the full automorphism group.
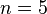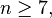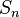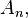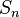For $n=5$ or $n \geq 7,$ the symmetric group $S_n$ is the automorphism group of the simple alternating group $A_n,$ so $S_n$ is almost simple in this trivial sense.
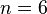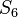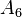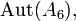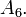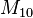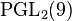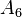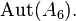
For $n=6$ there is a proper example, as $S_6$ sits properly between the simple $A_6$ and $\operatorname{Aut}(A_6),$ due to the exceptional outer automorphism of $A_6.$ Two other groups, the Mathieu group $M_{10}$ and the projective general linear group $\operatorname{PGL}_2(9)$ also sit properly between $A_6$ and $\operatorname{Aut}(A_6).$

Properties

The full automorphism group of a nonabelian simple group is a complete group (the conjugation map is an isomorphism to the automorphism group), but proper subgroups of the full automorphism group need not be complete.

Structure

By the Schreier conjecture, now generally accepted as a corollary of the classification of finite simple groups, the outer automorphism group of a finite simple group is a solvable group. Thus a finite almost simple group is an extension of a solvable group by a simple group.

Notes

External links

Almost simple group at the Group Properties wiki

This article is issued from Wikipedia - version of the 4/27/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.