Affirmative conclusion from a negative premise
Affirmative conclusion from a negative premise (illicit negative) is a formal fallacy that is committed when a categorical syllogism has a positive conclusion, but one or two negative premises.
For example:
- No fish are dogs, and no dogs can fly, therefore all fish can fly.
The only thing that can be properly inferred from these premises is that some things that are not fish cannot fly, provided that dogs exist.
Or:
- We don't read that trash. People who read that trash don't appreciate real literature. Therefore, we appreciate real literature.
This could be illustrated mathematically as
- If
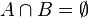and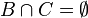 
then A ⊂ C.
It is a fallacy because any valid forms of categorical syllogism that assert a negative premise must have a negative conclusion.
See also
- Negative conclusion from affirmative premises, in which a syllogism is invalid because the conclusion is negative yet the premises are affirmative
- Fallacy of exclusive premises, in which a syllogism is invalid because both premises are negative
References
| ||||||||||||||||||||||
This article is issued from Wikipedia - version of the 6/11/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.